(本小题满分12分)某校数学课外兴趣小组为研究数学成绩是否与性别有关,先统计本校高三年级每个学生一学期数学成绩平均分(采用百分制),剔除平均分在30分以下的学生后,共有男生300名,女生200名.现采用分层抽样的方法,从中抽取了100名学生,按性别分为两组,并将两组学生成绩分为6组,得到如下所示频数分布表.
| 分数段 |
[40,50) |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
| 男 |
3 |
9 |
18 |
15 |
6 |
9 |
| 女 |
6 |
4 |
5 |
10 |
13 |
2 |
估计男、女生各自的成绩平均分(同一组数据用该组区间中点值作代表),从计算结果看,判断数学成绩与性别是否有关;
| |
优分 |
非优分 |
合计 |
| 男生 |
|
|
|
| 女生 |
|
|
|
| 合计 |
|
|
100 |
(2)规定80分以上为优分(含80分),请你根据已知条件作出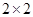 列联表,并判断是否有
列联表,并判断是否有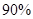 以上的把握认为“数学成绩与性别有关”.
以上的把握认为“数学成绩与性别有关”.
附表及公式
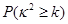 |
0.100 |
0.050 |
0.010 |
0.001 |
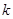 |
2.706 |
3.841 |
6.635 |
10.828 |
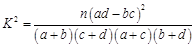 .
.
(本小题满分12分)
已知函数 的导数
的导数 满足
满足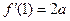 ,
,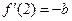 ,其中常数
,其中常数 ,求曲线
,求曲线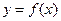 在点
在点 处的切线方程.
处的切线方程.
(本小题满分12分)已知二项式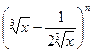 的展开式中,前三项系数的绝对值成等差数列.
的展开式中,前三项系数的绝对值成等差数列.
(I)求展开式的第四项;
(II)求展开式的常数项.
(本小题满分14分)
已知位于 轴右侧的圆C与
轴右侧的圆C与 相切于点P(0,1),与
相切于点P(0,1),与 轴相交于点A、B,且被
轴相交于点A、B,且被 轴分成的两段弧之比为1﹕2(如图所示).
轴分成的两段弧之比为1﹕2(如图所示).
(I)求圆C的方程;
(II)若经过点(1,0)的直线 与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线
与圆C相交于点E、F,且以线段EF为直径的圆恰好过圆心C,求直线 的方程.
的方程.
(本小题满分12分)
如图是函数 的一段图象.
的一段图象.
(I)求 的值及函数
的值及函数 的解析式;
的解析式;
(II)求函数 的最值及零点.
的最值及零点.
(本小题满分12分)
宏达电器厂人力资源部对本厂的一批专业技术人员的年龄状况和接受教育程度(学历)进行了调查,其结果如下表:
| 学历 |
35岁以下 |
35~50岁 |
50岁以上 |
| 本科 |
80 |
30 |
20 |
| 研究生 |
 |
20 |
 |
(Ⅰ)用分层抽样的方法在35~50岁年龄段的专业技术人员中抽取一个容量为5的样本,将该样本看成一个总体, 从中任取2人, 求至少有1人的学历为研究生的概率;
(Ⅱ)在该厂的专业技术人员中,按年龄用分层抽样的方法抽取 个人,其中35岁以下抽
个人,其中35岁以下抽
取48人,50岁以上抽取10人,再从这 个人中随机抽取出1人,此人的年龄为50岁以上
个人中随机抽取出1人,此人的年龄为50岁以上
的概率为 ,求
,求 、
、 的值.
的值.