已知抛物线
 ,准线与
,准线与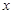 轴的交点为
轴的交点为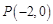 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)如图,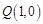 ,过点
,过点 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,AQ与BQ分别与抛物线
,AQ与BQ分别与抛物线 交于点
交于点
C,D,设AB,DC的斜率分别为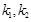 ,
,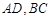 的斜率分别为
的斜率分别为 ,问:是否存在常数
,问:是否存在常数 ,使得
,使得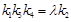 ,
,
若存在,求出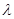 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(本小题满分12分)
已知甲船正在大海上航行。当它位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即以10海里/小时的速度匀速前往救援,同时把消息告知在甲船的南偏西30°,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用: )。
)。
(1) 试问乙船航行速度的大小;
(2) 试问乙船航行的方向(试用方位角表示,譬如北偏东…度)。
(本小题满分12分)
已知各项均为正数的数列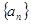 中,
中, 是数列
是数列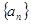 的前
的前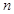 项和,对任意
项和,对任意 ,有
,有
(1)求常数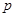 的值;
的值;
(2)求数列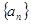 的通项公式;
的通项公式;
(3)记 ,求数列
,求数列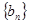 的前
的前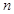 项和
项和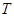 。
。
(本小题满分12分)
在直角坐标系中,一运动物体经过点A(0,9),其轨迹方程为y=ax2+c(a<0),D=(6,7)为x轴上的给定区间。
(1)为使物体落在D内,求a的取值范围;
(2)若物体运动时又经过点P(2,8.1),问它能否落在D内?并说明理由。
(本小题满分12分)
已知函数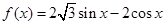 。
。
(1)若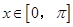 ,求
,求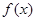 的最大值和最小值;
的最大值和最小值;
(2)若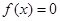 ,求
,求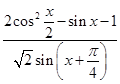 的值。
的值。
(本小题满分13分)
设函数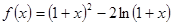 。
。
(1)求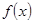 的单调区间;
的单调区间;
(2)若当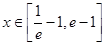 时,(其中
时,(其中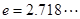 )不等式
)不等式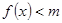 恒成立,求实数
恒成立,求实数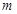 的取值范围;
的取值范围;
(3)试讨论关于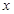 的方程:
的方程: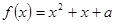 在区间
在区间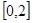 上的根的个数。
上的根的个数。