如图,有一四边形纸片ABCD,AB∥CD,AD∥BC,∠A=60°,将纸片分别沿折痕MN、PQ折叠,使点A与AB边上的点E重合,点C与CD边上的点F重合,EG平分∠MEB交CD于G,FH平分∠PFD交AB于H.试说明:
(1)EG∥FH;(2)ME∥PF.
先化简(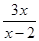 -
-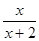 )·
)·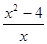 ,再选一个你喜欢的x的值代入求值。
,再选一个你喜欢的x的值代入求值。
如图,在平面直角坐标系xOy中,AB⊥x轴于点B,AB=3,tan∠AOB= ,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
,将△OAB绕着原点O逆时针旋转90°,得到△OA1B1;再将△OA1B1绕着线段OB1的中点旋转180°,得到△OA2B1,抛物线y=ax2+bx+c(a≠0)经过点B、B1、A2.
(1)求抛物线的解析式.
(2)在第三象限内,抛物线上的点P在什么位置时,△PBB1的面积最大?求出这时点P的坐标.
(3)在第三象限内,抛物线上是否存在点Q,使点Q到线段BB1的距离为 ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线.
(2)若BC=2 ,sin∠BCP=
,sin∠BCP= ,求点B到AC的距离.
,求点B到AC的距离.
(3)在第(2)的条件下,求△ACP的周长.
现有一块等腰三角形板,量得周长为32cm,底比一腰多2cm,若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请画出你能拼成的各种四边形的示意图,并计算拼成的各个四边形的两条对角线长的和.
如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?( ≈1.41,
≈1.41, ≈1.73,
≈1.73, =2.45).
=2.45).