(本小题12分)据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
| 态度 调查人群 |
应该取消 |
应该保留 |
无所谓 |
| 在校学生 |
2100人 |
120人 |
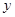 人 人 |
| 社会人士 |
600人 |
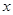 人 人 |
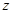 人 人 |
已知在全体样本中随机抽取 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为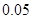
(1)现用分层抽样的方法在所有参与调查的人中抽取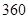 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)已知 ,
,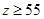 ,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
,若所选择的在校学生的人数低于被调查人群总数的80%,则认为本次调查“失效”,求本次调查“失效”的概率.
图中是抛物线型拱桥,当水面在 时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?
时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?
12分)已知函数y=xlnx
(1)求这个函数的导数;(2)求这个函数的图象在x=1点处的切线方程
如图,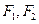 是双曲线
是双曲线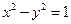 的两个焦点,O为坐标原点,圆
的两个焦点,O为坐标原点,圆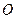 是以
是以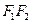 为直径的圆,直线
为直径的圆,直线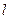 :
: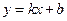 与圆O相切,并与双曲线交于A、B两点.
与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当 时,求直线
时,求直线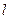 的方程;
的方程;
(Ⅲ)当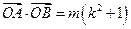 ,且满足
,且满足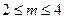 时,求
时,求 面积的取值范围.
面积的取值范围.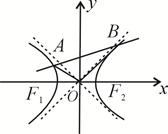
已知函数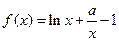 .
.
(Ⅰ)讨论函数的单调区间与极值;
(Ⅱ)当a=1时,是否存在过点(1,-1)的直线与函数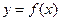 的图象相切?若存在,有多少条?若不存在,说明理由.
的图象相切?若存在,有多少条?若不存在,说明理由.
.湖南日报12月15日讯:今天,长沙飞起了今冬以来的第一场雪,省会城管部门采取措施抗冰除雪,确保道路畅通.铲雪车是铲冰除雪的主力,铲雪车行驶的费用分为两部分,第一部分是车的折旧费及其他服务费,每小时480元,第二部分为燃料费,它 与车速的立方成正比,并且当速度为10km/h时,燃料费为每小时30元.问车速为多少时,才能使行驶每公里的费用最小?并求出这个最小值以及此时每小时费用的总和.
与车速的立方成正比,并且当速度为10km/h时,燃料费为每小时30元.问车速为多少时,才能使行驶每公里的费用最小?并求出这个最小值以及此时每小时费用的总和.