(本小题满分12分)某校从参加某次知识竞赛的同学中,选取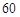 名同学将其成绩(百分制,均为整数)分成
名同学将其成绩(百分制,均为整数)分成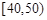 ,
,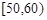 ,
,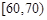 ,
, ,
, ,
, 六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.
六组后,得到频率分布直方图(如图),观察图形中的信息,回答下列问题.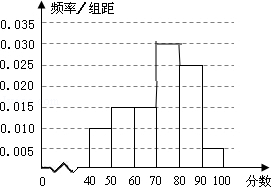
(1)从频率分布直方图中,估计本次考试成绩的中位数;
(2)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率.
(本小题满分12分)某工厂用 万元钱购买了一台新机器,运输安装费用
万元钱购买了一台新机器,运输安装费用 千元,每年投保、动力消耗的费用也为
千元,每年投保、动力消耗的费用也为 千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为
千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为 千元,第二年为
千元,第二年为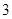 千元,第三年为
千元,第三年为 千元,依此类推,即每年增加
千元,依此类推,即每年增加 千元.
千元.
(Ⅰ)求使用 年后,保养、维修、更换易损零件的累计费用S(千元)关于
年后,保养、维修、更换易损零件的累计费用S(千元)关于 的表达式;
的表达式;
(Ⅱ)问这台机器最佳使用年限是多少年?并求出年平均费用(单位:千元)的最小值.(最佳使用年限是指使年平均费用最小的时间,年平均费用=(购入机器费用+运输安装费用+每年投保、动力消耗的费用+保养、维修、更换易损零件的累计费用)÷机器使用的年数 )
(本小题满分13分)(Ⅰ)若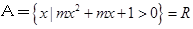 ,求实数
,求实数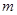 的取值范围;
的取值范围;
(Ⅱ)二次函数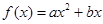 ,满足
,满足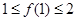 ,
,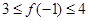 ,求
,求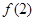 的取值范围.
的取值范围.
(本小题满分13分)(Ⅰ)已知数列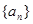 的前
的前 项和
项和 ,求通项公式
,求通项公式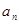 ;
;
(Ⅱ)已知等比数列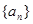 中,
中,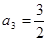 ,
,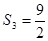 ,求通项公式
,求通项公式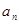
(本小题满分13分)角 分别是锐角
分别是锐角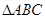 的三边
的三边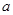 、
、 、
、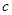 所对的角,
所对的角,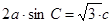 .
.
(Ⅰ)求角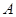 的大小;
的大小;
(Ⅱ)若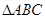 的面积
的面积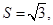 求
求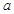 的最小值.
的最小值.
已知一个三角形的三边边长分别为2、3、4, 设计一个算法,求也它的面积。