(本小题满分12分)已知椭圆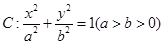 的离心率为
的离心率为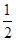 ,椭圆的短轴端点与双曲线
,椭圆的短轴端点与双曲线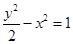 的焦点重合,过点
的焦点重合,过点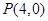 且不垂直于
且不垂直于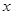 轴的直线
轴的直线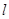 与椭圆
与椭圆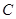 相交于
相交于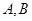 两点.
两点.
(1)求椭圆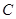 的方程;
的方程;
(2)求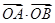 的取值范围.
的取值范围.
已知函数f(x)=x+ 的定义域为(0,+∞),且f(2)=2+
的定义域为(0,+∞),且f(2)=2+ .设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
.设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
(1)求a的值.
(2)问:|PM|•|PN|是否为定值?若是,则求出该定值;若不是,请说明理由.
(3)设O为坐标原点,求四边形OMPN面积的最小值.
已知圆C的方程为:x2+y2=4
(1)求过点P(2,1)且与圆C相切的直线l的方程;
(2)直线l过点D(1,2),且与圆C交于A、B两点,若|AB|=2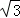 ,求直线l的方程;
,求直线l的方程;
(3)圆C上有一动点M(x0,y0), =(0,y0),若向量
=(0,y0),若向量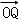 =
= +
+ ,求动点Q的轨迹方程.
,求动点Q的轨迹方程.
已知数列{an}的前n项和Sn=﹣ n2+kn(其中k∈N+),且Sn的最大值为8.
n2+kn(其中k∈N+),且Sn的最大值为8.
(1)确定常数k,求an;
(2)求数列 的前n项和Tn.
的前n项和Tn.
已知射线l1:y=4x(x≥0)和点P(6,4),试在l1上求一点Q使得PQ所在直线l和l1以及直线y=0在第一象限围成的面积达到最小值,并写出此时直线l的方程.
在△ABC中,a、b、c分别是角A、B、C的对边,且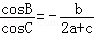 ,
,
(1)求角B的大小;
(2)若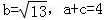 ,求△ABC的面积.
,求△ABC的面积.