(本小题满分12分)已知函数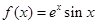
(1)求函数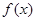 的单调区间;
的单调区间;
(2)当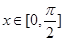 时,
时,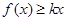 ,求实数
,求实数 的取值范围
的取值范围
某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x)万元,当年产量不足80千件时,C(x)=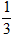 x2+10x(万元);当年产量不少于80千件时,C(x)=51x+
x2+10x(万元);当年产量不少于80千件时,C(x)=51x+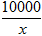 -1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
-1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
设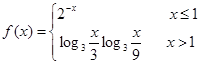 .
.
(1)求 的值;
的值;
(2)求 的最小值.
的最小值.
如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.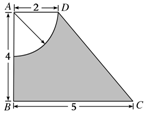
(1)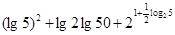 ;
;
(2)计算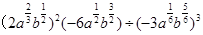 .
.
已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R}.若A∩B=[1,3],求实数m的值;