某厂生产某种产品的年固定成本为250万元，每生产x千件，需另投入成本为C（x）万元，当年产量不足80千件时，C（x）＝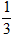
x2＋10x（万元）；当年产量不少于80千件时，C（x）＝51x＋
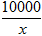－1 450（万元）．通过市场分析，若每件售价为500元时，该厂年内生产的商品能全部销售完．
（1）写出年利润L（万元）关于年产量x（千件）的函数解析式；
（2）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
设函数
.
(1)求函数
的单调区间和极值；
（2）若关于x的方程
有三个不同实根，求实数
的取值范围；
（3）已知当
恒成立，求实数k的取值范围。
已知函数
在
处取得极值，过点
作曲线
的切线
,（1）求此切线的方程.（2）求切线与函数
的图象围成的平面图形的面积。
某商场从生产厂家以每件20元购进一批商品，若该商品零售价定为p元，则销量Q（单位：件）与零售价p（单位：元）有如下关系：
.问该商品售价定为多少元时毛利润L最大，并求最大毛利润（毛利润=销售收入－进货支出）。
如图，在直三棱柱ABC－A1B1C1中，∠BAC＝90°，AB＝AC＝AA1＝1.D是棱CC1上的中点，P是AD的延长线与A1C1的延长线的交点.
(1)求二面角A－A1D－B的平面角的余弦值；
(2)求点C到平面B1DP的距离．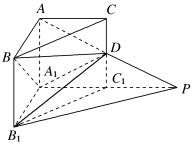
已知x、y为共轭复数，且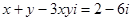
，求x、y.