（本小题满分12分）我们新定义一种三角形：两边平方和等于第三边平方的两倍的三角形叫做奇异三角形．
（1）根据“奇异三角形”的定义，请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
（2）在Rt△ABC中，∠ACB=90°，AB=c，AC=b，BC=a，且b>a，若Rt△ABC是奇异三角形，求a：b：c；
（3）如图，AB是⊙O的直径，C是⊙O上一点（不与点A，B重合），D是半圆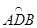
的中点，C，D在直径AB的两侧，若在⊙O内存在点E，使AE=AD，CB=CE．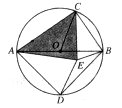
①求证：△ACE是奇异三角形；
②当△ACE是直角三角形时，求∠AOC的度数．
先化简，再求值：
，其中
，
.
计算
（1） 
（2）(
+
－
)×（－48）
（3）
（4）
（结果精确到0.01）
如图，纸上有五个边长为1的小正方形组成的图形，我们可以把它剪开拼成一个正方形。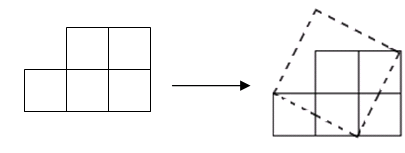
（1）拼成的正方形的面积与边长分别是多少？
（2）你能在3×3方格图中，连接四个格点组成面积为5的正方形吗？请在图中画出.
（3）如图，一只蚂蚁从一个棱长为1的立方体上点A爬到点B，再爬到点C，求路程（直接写出答案）
（4）上题中，蚂蚁从点A爬到点C有多条途径，其中有一条途径的路程是最短的，请你求出这一最短路程。
在数轴上，A点表示2，现在点A向右移动两个单位后到达点B；再向左移动10个单位到达C点：
（1）请在数轴上表示出A点开始移动时位置及B、C点位置；
（2）当A点移动到C点时，若要再移动到原点，问必须向哪个方向移动多少个单位？
（3）请把A点从开始移动直至到达原点这一过程，用一个有理数算式表达出来.
先观察：
，
，
，
.
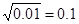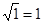（1）从题中的例子发现，当被开方数的小数点向一个方向移动2位时，算术平方根的小数点向相同方向移动位；
（2）已知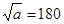
，
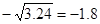，则
；
（3）已知
≈1.442，则
≈.