如图是一个圆锥与其侧面展开图,已知圆锥的底面半径是2,母线长是6.
(1)求这个圆锥的高和其侧面展开图中∠ABC的度数;
(2)如果A是底面圆周上一点,从点A拉一根绳子绕圆锥侧面一圈再回到A点,求这根绳子的最短长度.
已知点P(1,-2a)在二次函数y=ax2+6的图象上,并且点P关于x轴的对称点在反比例函数 的图象上。
的图象上。
(1)求此二次函数和反比例函数的解析式;
(2)点(-1,4)是否同时在(1)中的两个函数图象上?
正方形网格中,小格的顶点叫做格点。三个顶点都在网格格点上的三角形叫做格点三角形。小华已在左边的正方形网格中作出一个格点三角形。请你在其他两个正方形网格中各画出一个不同的格点三角形,使得三个网格中的格点三角形都相似(不包括全等).
如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接 AE.AC和BE相交于点O.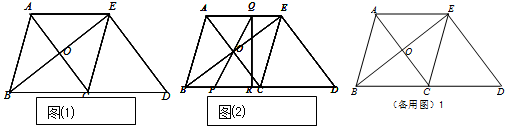
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AB于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,△PQR与△BOC相似?
当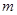 为什么值时,关于
为什么值时,关于 的方程
的方程 有实根。
有实根。