在空间直角坐标系中,哪个坐标平面与x轴垂直?哪个平面与y轴垂直?哪个坐标平面与z轴垂直?
已知圆C: ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。
设圆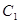 的方程为
的方程为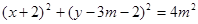 ,直线
,直线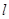 的方程为
的方程为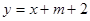 .
.
(1)求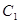 关于
关于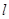 对称的圆
对称的圆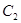 的方程;
的方程;
(2)当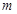 变化且
变化且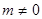 时,求证:
时,求证: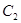 的圆心在一条定直线上,并求
的圆心在一条定直线上,并求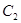 所表示的一系列圆的公切线方程.
所表示的一系列圆的公切线方程.
设正方形ABCD的外接圆方程为x2+y2–6x+a=0(a<9),C、D点所在直线l的斜率为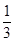 ,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。
,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。
已知圆C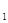 :x
:x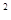 +y
+y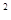 +2x-6y+1=0,圆C
+2x-6y+1=0,圆C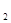 :x
:x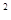 +y
+y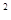 -4x+2y-11=0,求两圆的公共弦所在的直线方程及公共弦长.
-4x+2y-11=0,求两圆的公共弦所在的直线方程及公共弦长.