在一个不透明的口袋中装有大小、外形等一模一样的5个红球,3个兰球和2个白球,它们已经在口袋中搅匀了,请判断以下事件是“必然发生”、“随机发生”、还是“不可能发生”的?并说明理由.
(1)从口袋中任意取出5个球,只有兰球和白球,没有红球;
(2)从口袋中任意取出5个球,恰好兰球、白球、红球三种颜色都齐全了;
(3)从口袋中一次取出5个球,全是兰球.
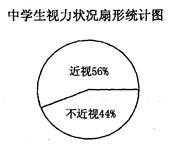
本市青少年健康研究中心随机抽取了全市1000名小学生和若干名中学生,对他们的视力状况进行了调查,并把调查结果绘制成如下统计图(近视程度分为轻度、中度、高度三种)。
(1)求这1000名小学生患近视的百分比;
(2)求本次抽查的中学生人数;
(3)该市有中学生8万人,小学生10万人。分别估计该市的中学生与小学生患“中度近视”的人数;
(4)将这1000名小学生的视力状况(包括近视程度)绘制成扇形统计图。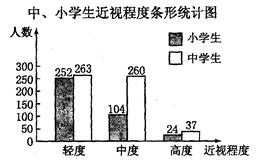
在长方形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示。试求图中阴影部分的总面积。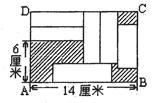
一列火车从北京出发到达广州大约需要15小时。火车出发后先按原来的时速匀速行驶8小时后到达武汉,由于2009年12月世界时速最高铁路武广高铁正式投入运营,现在从武汉到广州火车的平均时速是原来的2倍还多50公里,所需时间也比原来缩短了4个小时。求火车从北京到武汉的平均时速和提速后武汉到广州的平均时速。
若a,b为有理数,且满足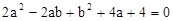 ,
,
求: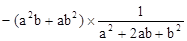 的值。
的值。
已知 ,求
,求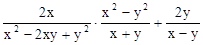 的值。
的值。