(18分)如图所示,倾斜角θ=30°的光滑倾斜导体轨道(足够长)与光滑水平导体轨道连接.轨道宽度均为L=1m,电阻忽略不计.匀强磁场I仅分布在水平轨道平面所在区域,方向水平向右,大小B1=1T;匀强磁场II仅分布在倾斜轨道平面所在区域,方向垂直于倾斜轨道平面向下,大小B2=1T.现将两质量均为m=0.2kg,电阻均为R=0.5Ω的相同导体棒ab和cd,垂直于轨道分别置于水平轨道上和倾斜轨道上,并同时由静止释放.取g=10m/s2.
(1)求导体棒cd沿斜轨道下滑的最大速度的大小;
(2)若已知从开始运动到cd棒达到最大速度的过程中,ab棒产生的焦耳热Q=0.45J,求该过程中通过cd棒横截面的电荷量;
(3)若已知cd棒开始运动时距水平轨道高度h=10m,cd棒由静止释放后,为使cd棒中无感应电流,可让磁场Ⅱ的磁感应强度随时间变化,将cd棒开始运动的时刻记为t=0,此时磁场Ⅱ的磁感应强度为B0=1T,试求cd棒在倾斜轨道上下滑的这段时间内,磁场Ⅱ的磁感应强度B随时间t变化的关系式.
一辆车在水平光滑路面上以速度v匀速行驶.车上的人每次以相同的速度4v(对地速度)向行驶的正前方抛出一个质量为m的沙包.抛出第一个沙包后,车速减为原来的 ,则抛出第四个沙包后,此车的运动情况如何?
,则抛出第四个沙包后,此车的运动情况如何?
如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y 轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E。初速可忽略的电子经过一个电势差U未确定的电场直线加速后,从y轴上的A点以垂直于电场的方向射入第一象限区域,A点坐标为(0,h),已知电子的电量为e,质量为m,(重力忽略不计),若电子可以在第一象限从MN边界离开电场区域,求: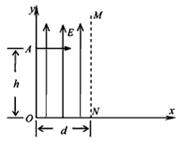
(1)加速电场的电势差要满足的条件;
(2)若满足上述条件的加速电场的电势差为U0时,求电子经过x轴时离坐标原点O的距离X。
如图所示电路中,一直流电动机与阻值R=9Ω的电阻串联接在电源上。电源电动势E=20V、内阻r=1Ω,用理想电压表测出电动机两端的电压U=10V。已知电动机线圈电阻RM=1Ω,求:
(1)电路中的电流为多少?
(2)电动机输出的功率为多少?
(3)电动机的效率?
如图所示电路中,电源电动势E=" 12V" ,内电阻r =" 1.0Ω" ,电阻R1=9.0Ω,R2= 15Ω,电流表A示数为0.40A ,求电阻R3的阻值和它消耗的电功率。
把质量m的带负电小球A,用绝缘细绳悬起,若将带电荷量为Q的带正电球B靠近A,当两个带电小球在同一高度相距r时,绳与竖直方向成α角.试求:
(1)A球受到的绳子拉力多大?
(2)A球带电荷量是多少?