已知：关于x的方程x2﹣（k+2）x+2x=0
（1）求证：无论取任何实数值，方程总有实数根；
（2）若等腰三角形ABC的一边长a=1，另两边长b，c恰好是这个方程的两个根，求△ABC的周长．
（本小题满分8分）如图，在一面与地面垂直的围墙的同一侧有一根高10米的旗杆AB和一个高度未知的电线杆CD，它们都与地面垂直。为了测得电线杆的高度，一个小组的同学进行了如下测量：某一时刻，在太阳光的照射下，旗杆落在围墙上的影子EF的长度为2米，落在地面上的影子BF的长为10米；而电线杆落在围墙上的影子GH的长度为3米，落在地面上的影子DH的长为5米。依据这些数据，该小组的同学计算出了电线杆的高度。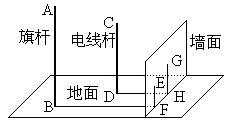
（1）该小组的同学在这里利用的是____________投影的有关知识进行计算的；
（2）试计算出电线杆的高度，并写出计算的过程。
如图，平行四边形ABCD中，AB=3cm,BC=5cm,∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．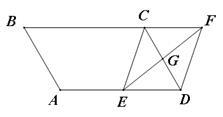
（1）求证：四边形CEDF是平行四边形；
（2）①当AE= cm时，四边形CEDF是矩形；
②当AE= cm时，四边形CEDF是菱形；（直接写出答案，不需要说明理由）
（贵州省安顺市）（本题12分）
如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF//AB交AC于F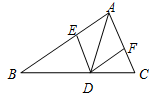
（1）求证：AE=DF．
（2）若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．
（内蒙古 呼 和 浩 特 ）如图，
ABCD的对角线AC、BD相交于点O，AE=CF．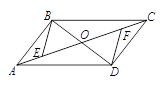
（1）求证：△BOE ≌△DOF ;
（2）若BD=EF，连接DE、BF，判断四边形EBFD的形状，无需说明理由．
（贵州六盘水）(本小题12分)如图，已知Rt△ACB中，∠C＝90°，∠BAC＝45°．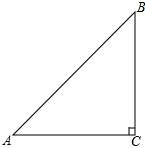
（1）用尺规作图，：在CA的延长线上截取AD＝AB，并连接BD（不写作法，保留作图痕迹）
（2）求∠BDC的度数．
（3）定义：在直角三角形中，一个锐角A的邻边与对边的比叫做∠A的余切，记作cotA，即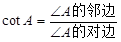
，根据定义，利用图形求cot22．5°的值．