(贵州省安顺市)(本题12分)
如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF//AB交AC于F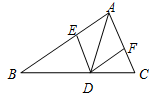
(1)求证:AE=DF.
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
已知: 是等腰直角三角形, ,将 绕点 顺时针方向旋转得到△ ,记旋转角为 ,当 时,作 ,垂足为 , 与 交于点 .
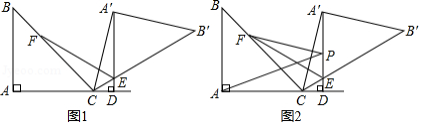
(1)如图1,当 时,作 的平分线 交 于点 .
①写出旋转角 的度数;
②求证: ;
(2)如图2,在(1)的条件下,设 是直线 上的一个动点,连接 , ,若 ,求线段 的最小值.(结果保留根号)
如图,已知抛物线 的顶点为 ,与 轴相交于点 ,对称轴为直线 ,点 是线段 的中点.
(1)求抛物线的表达式;
(2)写出点 的坐标并求直线 的表达式;
(3)设动点 , 分别在抛物线和对称轴 上,当以 , , , 为顶点的四边形是平行四边形时,求 , 两点的坐标.

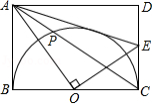
如图,在矩形 中,以 边为直径作半圆 , 交 边于点 ,对角线 与半圆 的另一个交点为 ,连接 .
(1)求证: 是半圆 的切线;
(2)若 , ,求 的长.
为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的 ,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩 分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
|
分数段(分 |
频数(人 |
频率 |
|
|
|
0.1 |
|
|
18 |
0.18 |
|
|
|
|
|
|
35 |
0.35 |
|
|
12 |
0.12 |
|
合计 |
100 |
1 |
(1)填空: , , ;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为 的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为 ,请你估算全校获得二等奖的学生人数.
