如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,4),抛物线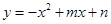 经过点A和C.
经过点A和C.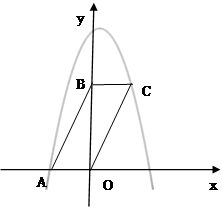
(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为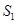 ,右侧部分图形的面积记为
,右侧部分图形的面积记为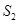 ,求
,求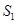 与
与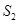 的比.
的比.
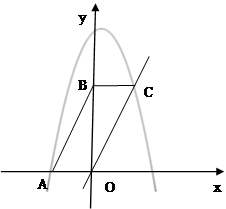
(3)在y轴上取一点D,坐标是(0,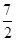 ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到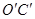 ,点D关于直线
,点D关于直线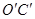 的对称点记为
的对称点记为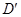 ,当点
,当点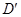 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点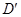 坐标并直接写出直线
坐标并直接写出直线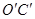 的函数解析式.
的函数解析式.
如图1,在 中, , , ,点 、 分别是边 、 的中点,连接 .将 绕点 逆时针方向旋转,记旋转角为 .
(1)问题发现
①当 时, ;
②当 时, .
(2)拓展探究
试判断:当 时, 的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
绕点 逆时针旋转至 、 、 三点在同一条直线上时,求线段 的长.

为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个电子产品的固定成本为100元,问这种电子产品降价后的销售单价为多少元时,公司每天可获利32000元?
如图,在平面直角坐标系中,直线 与双曲线 相交于 、 两点, 轴,垂足为 , 的面积是2.
(1)求 、 的值;
(2)求直线 的解析式.

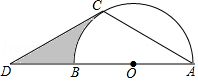
如图, 是 的直径,点 是 延长线上的一点,点 在 上,且 , .
(1)求证: 是 的切线;
(2)若 的半径为3,求图中阴影部分的面积.
为庆祝建国70周年,东营市某中学决定举办校园艺术节.学生从“书法”、“绘画”、“声乐”、“器乐”、“舞蹈”五个类别中选择一类报名参加.为了了解报名情况,组委会在全校随机抽取了若干名学生进行问卷调查,现将报名情况绘制成如图所示的不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)补全条形统计图;
(3)在扇形统计图中,求“声乐”类对应扇形圆心角的度数;
(4)小东和小颖报名参加“器乐”类比赛,现从小提琴、单簧管、钢琴、电子琴四种乐器中随机选择一种乐器,用列表法或画树状图法求出他们选中同一种乐器的概率.
