【选修4—4:坐标系与参数方程】(本小题满分10分)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合.曲线C的极坐标方程为 ,直线l的参数方程为
,直线l的参数方程为 (t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
(t为参数,t∈R).试在曲线C上求一点M,使它到直线l的距离最大.
某体育兴趣小组共有A、B、C、D、E五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
| A |
B |
C |
D |
E |
|
| 身高 |
1.69 |
1.73 |
1.75 |
1.79 |
1.82 |
| 体重 |
19.2 |
25.1 |
18.5 |
23.3 |
20.9 |
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
已知函数 的图象过点
的图象过点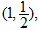 且点
且点
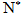 )在函数
)在函数 的图象上.
的图象上.
(1)求数列{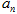 }的通项公式;
}的通项公式;
(2)令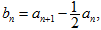 若数列{
若数列{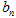 }的前n项和为
}的前n项和为 求证:
求证: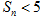 .
.
在△ABC中,内角A、B、C对边的边长分别是a、b、c.已知c=2,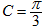 .
.
(1)若△ABC的面积等于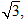 求a与b的值;
求a与b的值;
(2)若sinB=2sinA,求△ABC的面积.
为方便游客出行,某旅游点有50辆自行车供租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超过6元,则每超过1元,租不出的自行车就增加3辆.为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日出租自行车的总收入减去管理费用后的所得).
(1)求函数y=f(x)的解析式及其定义域;
(2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
如图所示,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.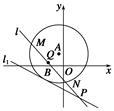
(1)求圆A的方程;
(2)当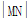 =2
=2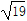 时,求直线l的方程;
时,求直线l的方程;
(3)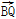 ·
·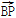 是否为定值?如果是,求出其定值;如果不是,请说明理由.
是否为定值?如果是,求出其定值;如果不是,请说明理由.