(本小题满分14分)已知函数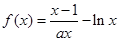 (
(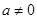 )
)
(Ⅰ)求函数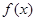 的单调区间;
的单调区间;
(Ⅱ)当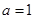 时,求
时,求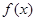 在
在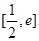 上的最大值和最小值(
上的最大值和最小值( );
);
(Ⅲ)求证: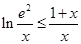 .
.
为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: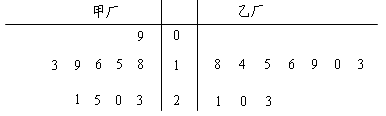
规定:当产品中的此种元素含量不小于18毫克时,该产品为优等品.
(1)试用上述样本数据估计甲、乙两厂生产的优等品率;
(2)从乙厂抽出的上述10件样品中,随机抽取3件,求抽到的3件样品中优等品数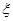 的分布列及其数学期望
的分布列及其数学期望 ;
;
(3)从甲厂的10件样品中有放回的随机抽取3件,也从乙厂的10件样品中有放回的随机抽取3件,求抽到的优等品数甲厂恰比乙厂多2件的概率.
在 中,角
中,角 的对边分别为
的对边分别为 向量
向量 ,
, ,且
,且 .
.
(1)求 的值;
的值;
(2)若 ,
,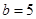 ,求角
,求角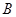 的大小及向量
的大小及向量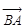 在
在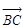 方向上的投影.
方向上的投影.
已知函数 (
(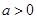 ).
).
(1)当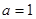 时,求函数
时,求函数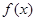 的单调区间;
的单调区间;
(2)当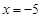 时,
时,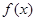 取得极值,求函数
取得极值,求函数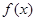 在
在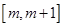
 上的最小值;
上的最小值;
已知抛物线的顶点在坐标原点,焦点在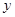 轴上,且过点
轴上,且过点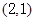 .
.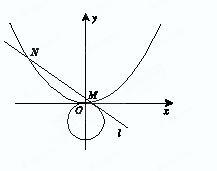
(1)求抛物线的标准方程;
(2)与圆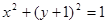 相切的直线
相切的直线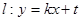 交抛物线于不同的两点
交抛物线于不同的两点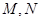 若抛物线上一点
若抛物线上一点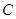 满足
满足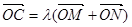
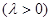 ,求
,求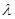 的取值范围.
的取值范围.
已知函数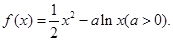
(1)若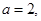 求
求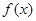 在
在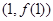 处的切线方程;
处的切线方程;
(2)若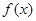 在区间
在区间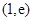 上恰有两个零点,求
上恰有两个零点,求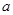 的取值范围.
的取值范围.