(本小题满分12分)《中国足球改革发展总体方案》明确指出:加强对国家队经费投入、奖励政策、基地建设、后勤服务、情报信息等 方面的保障,提高服务水平。新建2个国家足球训练基地,满足国家队不同季节的比赛和训练需要。有关机构分别对甲、乙两个地区的7个城市进行评估量化,它们的量化分数的茎叶图如图所示,其中甲地区城市的平均量化分为85,乙地区城市的中位数为83.
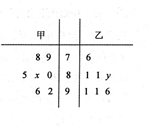
(Ⅰ)求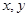 的值;
的值;
(Ⅱ)从量化分在90分以上的城市中随机抽取两个城市,求乙地区至少有一个城市的概率.
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A,B的一点,D为AC的中点. 
(1)求该圆锥的侧面积S;
(2)求证:平面PAC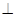 平面POD;
平面POD;
(3)若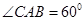 ,在三棱锥A-PBC中,求点A到平面PBC的距离.
,在三棱锥A-PBC中,求点A到平面PBC的距离.
已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求概率P
,求概率P .
.
(2)在正方形ABCD内部随机取一点P,求满足 的概率.
的概率.
已知函数
(1)求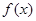 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)已知 是
是 三边长,且
三边长,且 ,
, 的面积
的面积 .求角
.求角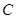 及
及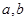 的值.
的值.
已知函数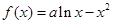 .
.
(1)当 时,求函数
时,求函数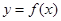 在
在 上的最大值;
上的最大值;
(2)令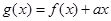 ,若
,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数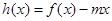 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且 ,又
,又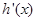 是
是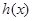 的导函数,若正常数
的导函数,若正常数 满足条件
满足条件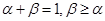 .证明:
.证明: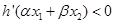 .
.
 的内切圆与三边
的内切圆与三边 的切点分别为
的切点分别为 ,已知
,已知 ,内切圆圆心
,内切圆圆心 ,设点A的轨迹为R.
,设点A的轨迹为R. 
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.