下列命题错误的是( )
A.如果平面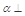 平面 平面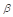 ,那么平面 ,那么平面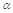 内一定存在直线平行于平面 内一定存在直线平行于平面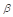 |
B.如果平面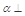 平面 平面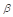 ,那么平面 ,那么平面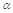 内所有直线都垂直于平面 内所有直线都垂直于平面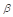 |
C.如果平面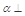 平面 平面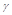 ,平面 ,平面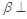 平面 平面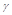 , ,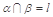 那么 那么 平面 平面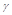 |
D.如果平面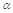 不垂直于平面 不垂直于平面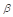 ,那么平面 ,那么平面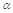 内一定不存在直线垂直于平面 内一定不存在直线垂直于平面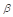 |
甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为 ,且各局胜负相互独立,则比赛停止时已打局数
,且各局胜负相互独立,则比赛停止时已打局数 的期望
的期望 为()
为()
A. |
B. |
C. |
D. |
在 中,已知
中,已知 ,
,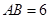 ,若
,若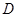 点在斜边
点在斜边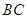 上,
上,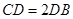 ,则
,则 的值为()
的值为()
| A.48 | B.24 | C.12 | D.6 |
将二项式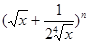 的展开式按
的展开式按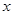 的降幂排列,若前三项系数成等差数列,则该展开
的降幂排列,若前三项系数成等差数列,则该展开
式中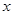 的指数是整数的项共有()个
的指数是整数的项共有()个
| A.3 | B.4 | C.5 | D.6 |
给定下列两个关于异面直线的命题:那么()
命题(1):若平面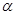 上的直线
上的直线 与平面
与平面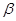 上的直线
上的直线 为异面直线,直线
为异面直线,直线 是
是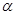 与
与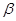 的交线,那么
的交线,那么 至多与
至多与 中的一条相交;
中的一条相交;
命题(2):不存在这样的无穷多条直线,它们中的任意两条都是异面直线.
| A.命题(1)正确,命题(2)不正确 |
| B.命题(2)正确,命题(1)不正确 |
| C.两个命题都正确 |
| D.两个命题都不正确 |
一几何体的三视图如图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为()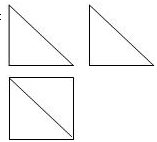
A.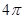 |
B.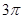 |
C.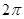 |
D.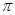 |