某市举行青年教师数学解题大赛,从中随机抽取30名老师,将他们的竞赛成绩(满分100分,成绩均为不低于30分的整数)分成六段: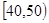 ,
,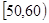 , ,
, ,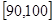 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.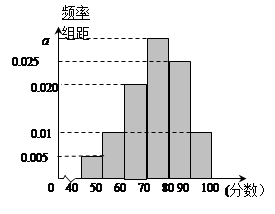
(Ⅰ)在这30名老师中随机抽取3名老师.求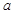 的值,以及同时满足下列两个条件的概率:①有且仅有1名老师成绩不低于90分;②成绩在
的值,以及同时满足下列两个条件的概率:①有且仅有1名老师成绩不低于90分;②成绩在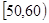 内至多1名老师;
内至多1名老师;
(Ⅱ)在成绩在 内的老师中随机抽取3名老师进行诊断调查,设成绩在
内的老师中随机抽取3名老师进行诊断调查,设成绩在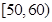 内的人数为随机变量
内的人数为随机变量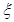 ,求
,求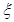 的分布列及其期望.
的分布列及其期望.
已知 为锐角,且
为锐角,且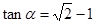 ,函数
,函数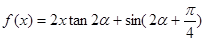 ,数列{
,数列{ }的首项
}的首项 .
.
(1)求函数 的表达式;
的表达式;
(2)求数列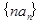 的前
的前 项和
项和 .
.
 的外接圆半径
的外接圆半径 ,角
,角 的对边分别是
的对边分别是 ,且
,且
(1)求角 和边长
和边长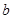 ;
;
(2)求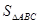 的最大值及取得最大值时的
的最大值及取得最大值时的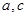 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.
已知函数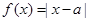 .
.
(1)若 的解集为
的解集为 ,求实数
,求实数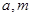 的值.
的值.
(2)当 且
且 时,解关于
时,解关于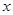 的不等式
的不等式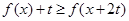 .
.
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.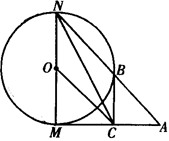
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
已知函数f(x)=alnx+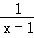 (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若x1∈(0, ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x1)﹣f(x2)≥ln2+
,2]时,求证:f(x1)﹣f(x2)≥ln2+ .
.