如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,点F是CD的中点,且AF⊥AB,若AD=2.7,AF=4,AB=6,求CE的长.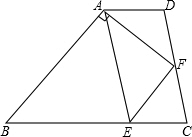
如图1,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.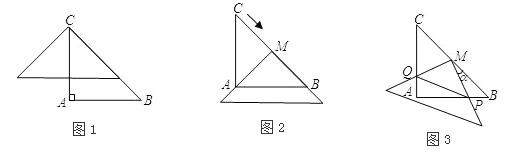
(1)操作1:固定△ABC,将三角板沿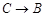 方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿
方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿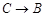 方向平移的距离为___________;
方向平移的距离为___________;
(2)操作2:在(1)的情况下,将三角板沿着BC的中点M顺时针方向旋转角度 ,如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
,如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;
(3)在(2)的情形下,连PQ,设BP=x,记△MPQ的面积为y,试求y关于x的函数关系式,并求x为何值时,y的值是四边形MPAQ的面积的一半,此时,指出四边形MPAQ的形状.
如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).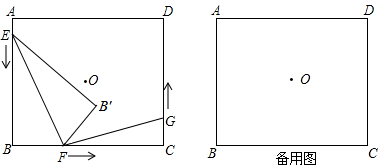
(1)当t= s时,四边形EBFB′为正方形;
(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.
如图,在矩形ABCO中,AO=3,tan∠ACB=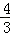 .以O为坐标原点,OC为x轴,OA为y轴建立平面直角坐标系,设D、E分别是线段AC、OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动.设运动时间为t(秒)
.以O为坐标原点,OC为x轴,OA为y轴建立平面直角坐标系,设D、E分别是线段AC、OC上的动点,它们同时出发,点D以每秒3个单位的速度从点A向点C运动,点E以每秒1个单位的速度从点C向点O运动.设运动时间为t(秒)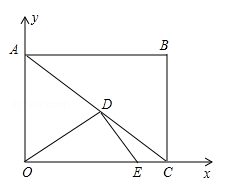
(1)求直线AC的解析式;
(2)用含t的代数式表示点D的坐标;
(3)在t为何值时,△ODE为直角三角形?
(4)在什么条件下,以Rt△ODE的三个顶点能确定一条对称轴平行于y轴的抛物线?并请选择一种情况,求出所确定的抛物线的解析式.
如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB= ,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).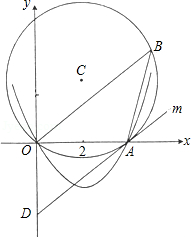
(1)求抛物线的函数解析式;
(2)直线m与⊙C相切于点A,交y轴于点D.动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值;
(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标.
在平面直角坐标系xOy中,已知动点P在正比例函数y=x的图象上,点P的横坐标为m(m>0),以点P为圆心, m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(点D在点C的上方).点E为平行四边形DOPE的顶点(如图).
m为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(点D在点C的上方).点E为平行四边形DOPE的顶点(如图).
(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ,试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC﹣∠DBE的度数.