如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，n）在边AB上，反比例函数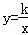
（k≠0）在第一象限内的图象经过点D、E，且D点的横坐标是它的纵坐标的2倍．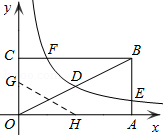
（1）求边AB的长；
（2）求反比例函数的解析式和n的值；
（3）若反比例函数的图象与矩形的边BC交于点F，将矩形折叠，使点O与点F重合，折痕分别与x、y轴正半轴交于点H、G，求线段OG的长．
（1）计算
（2）解方程
在平面直角坐标系
中，对于任意三点
、
、
的“矩面积”，给出如下定义：“水平底”
：任意两点横坐标差的最大值，“铅垂高”
：任意两点纵坐标差的最大值，则“矩面积”
．
例如：三点坐标分别为
，
，
，则“水平底”
，“铅垂高”
，“矩面积”
．
（1）已知点
，，
．
①若、、
三点的“矩面积”为
，求点的坐标；
②、、三点的“矩面积”的最小值为
（2）已知点
，
，
，其中
．若
、
、
三点的“矩面积”的为8，求
的取值范围；
如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动
点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1．25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：
（1）求点N的坐标（用含x的代数式表示）；
（2）设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少？
（3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由．
数学兴趣小组测量校园内旗杆的高度，有以下两种方案：
方案一：小明在地面直上立一根标杆EF，沿着直线BF后退到点D，使眼睛C、标杆的顶点E 、旗杆的
顶点A在同一直线上（如图1）．测量：人与标杆的距离DF=1m，人与旗杆的距离DB=16m，人的目高
和标杆的高度差EG=0．9m，人的高度CD=1．6m．
方案二：小聪在某一时刻测得1米长的竹竿竖直放置时影长1．5米，在同时刻测量旗杆的影长时，因
旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙
上的影高为2米（如图2）．
请你结合上述两个方案，分别画出符合题意的示意图，并求出旗杆的高度．
如图，△ABC是等边三角形，D、E在BC边所在的直线上，且BC2=BD•CE．
（1）求∠DAE的度数
（2）求证：AD2=DB•DE