(8分)
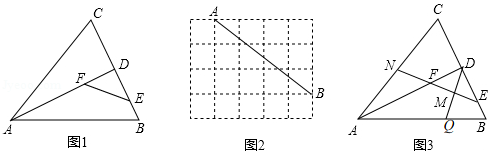
如上右图,在Rt△ABC中,∠ B=90°,E为AB上一点,∠ C=∠BEO,O是BC上一点,以D为圆心,OB长为半径作⊙O,,AC是⊙O,的切线.
(1)求证:OE=OC;
(2)若BE=4,BC=8,求OE的长.
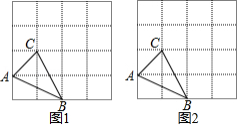
如图,在 的方格子中, 的三个顶点都在格点上.
(1)在图1中画出线段 ,使 ,其中 是格点.
(2)在图2中画出平行四边形 ,其中 是格点.
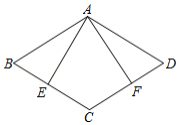
已知:如图,在菱形 中,点 , 分别在边 , 上,且 ,连结 , .求证: .
计算: .
如图1, 经过等边 的顶点 , (圆心 在 内),分别与 , 的延长线交于点 , ,连结 , 交 于点 .
(1)求证: .
(2)当 , 时,求 的长.
(3)设 , .
①求 关于 的函数表达式;
②如图2,连结 , ,若 的面积是 面积的10倍,求 的值.
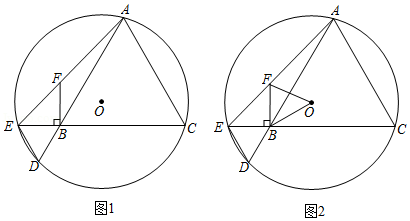
定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
(1)如图1,在 中, , 是 的角平分线, , 分别是 , 上的点.
求证:四边形 是邻余四边形.
(2)如图2,在 的方格纸中, , 在格点上,请画出一个符合条件的邻余四边形 ,使 是邻余线, , 在格点上.
(3)如图3,在(1)的条件下,取 中点 ,连结 并延长交 于点 ,延长 交 于点 .若 为 的中点, , ,求邻余线 的长.