某流域综合治理工程已正式启动,其中某项工程,若由甲、乙两建筑队合做,6个月可以完成,若由甲、乙两队独做,甲队比乙队少用5个月的时间完成.
(1)甲、乙两队单独完成这项工程各需几个月的时间?
(2)已知甲队每月施工费用为15万元,比乙队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲队做a个月,乙队做b个月(a、b均为整数)分工合作的方式施工,问有哪几种施工方案?
平面直角坐标系中,顺次连结(-2,1),(-2,-1),(2,-2),(2,3)各点,你会得到
一个什么图形?试求这个图形的面积.
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒).设△BPQ的面积为S,求S与t之间的函数关系式
当线段PQ与线段AB相交于点O,且2AO=OB时,求t的值.
当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.

在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.
甲、乙两地之间的距离为 km,乙、丙两地之间的距离为 km;

求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?

求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
如图,在平面直角坐标系中,△ ABC的三个顶点的坐标分别为A(0,1),B(-1,1),C(-1,3)。画出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2,并写出点C2的坐标;,
将△A2B2C2平移得到△ A3B3C3,使点A2的对应点是A3,点B2的对应点是B3,点C2的对应点是C3(4,-1),在坐标系中画出△ A3B3C3,并写出点A3,B3的坐标。

2011年5月上旬,无锡市共有35000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成如图所示的扇形图和统计表: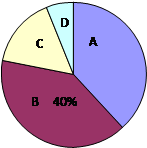
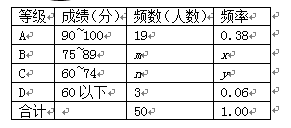
请你根据以上图表提供的信息,解答下列问题: m=,n=,x=,y=;
在扇形图中,C等级所对应的圆心角是度;
如果该校九年级共有500名男生参加了立定跳远测试,那么请你估计这些男生成绩等级达到优秀和良好的共有多少人?