如图甲所示，一个质量m＝0.1kg的正方形金属框总电阻R＝0-优题课

题文

如图甲所示，一个质量m＝0.1kg的正方形金属框总电阻R＝0.5 Ω，金属框放在表面绝缘的斜面AA′B′B的顶端(金属框上边与AA′重合)，自静止开始沿斜面下滑，下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与BB′重合)，设金属框在下滑过程中的速度为v，与此对应的位移为x，那么v²-x图象如图乙所示，已知匀强磁场方向垂直斜面向上，金属框与斜面间的动摩擦因数μ＝0.5，斜面倾角θ=53°取g＝10 m/s²，sin53°= 0.8，cos53°= 0.6。求：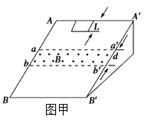

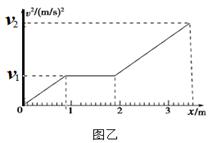
（1）金属框下滑加速度a和进入磁场的速度v₁
（2）金属框经过磁场时受到的安培力F_A大小和产生的电热Q
（3）匀强磁场的磁感应强度大小B

科目物理题型计算题难度较难

知识点：放射性同位素的应用

登录免费查看答案和解析

相关试题

由三颗星体构成的系统，忽略其他星体对它们的作用，存在着一种运动形式:三颗星体在相互之间的万有引力作用下，分别位于等边三角形的三个顶点上，绕某一共同的圆心 $O$ 在三角形所在的平面内做相同角速度的圆周运动（图示为 $A$ 、 $B$ 、 $C$ 三颗星体质量不相同时的一般情况）。若A星体质量为 $2 m$ ， $B$ 、 $C$ 两星体的质量均为 $m$ ，三角形边长为 $a$ 。求：

（1） $A$ 星体所受合力大小 $F_{A}$ ；

（2） $B$ 星体所受合力大小 $F_{B}$ ；
（3） $C$ 星体的轨道半径 $R_{C}$ ；
（4）三星体做圆周运动的周期 $T$ 。

在 $x O y$ 平面内，有沿 $y$ 轴负方向的匀强电场，场强大小为 $E$ （图中未画出），由 $A$ 点斜射出一质量为 $m$ ，带电荷量为 $+ q$ 的粒子， $B$ 和 $C$ 是粒子运动轨迹上的两点，如图所示，其中 $l_{0}$ 为常数。粒子所受重力忽略不计。求：

（1）粒子从 $A$ 到 $C$ 过程中电场力对它做的功；
（2）粒子从 $A$ 到 $C$ 过程所经历的时间；
（3）粒子经过 $C$ 点时的速率。

一质量为0.5 $k g$ 的小物块放在水平地面上的 $A$ 点，距离 $A$ 点5 $m$ 的位置 $B$ 处是一面墙，如图所示。长物块以 $v_{0}$ ="9" $m / s$ 的初速度从 $A$ 点沿 $A B$ 方向运动，在与墙壁碰撞前瞬间的速度为7 $m / s$ ，碰后以6 $m / s$ 的速度把向运动直至静止。 $g$ 取10 $m / s$ ²。

（1）求物块与地面间的动摩擦因数 $μ$ ；
（2）若碰撞时间为0.05 $s$ ，求碰撞过程中墙面对物块平均作用力的大小 $F$ ；
（3）求物块在反向运动过程中克服摩擦力所做的功 $W$ 。

(14分)如图所示为一传送带装置模型，斜面的倾角θ，底端经一长度可忽略的光滑圆弧与足够长的水平传送带相连接，质量m="2kg" 的物体从高h=30cm的斜面上由静止开始下滑，它与斜面的动摩擦因数μ₁=0.25，与水平传送带的动摩擦因数μ₂=0.5，物体在传送带上运动一段时间以后，物体又回到了斜面上，如此反复多次后最终停在斜面底端。已知传送带的速度恒为v=2.5m/s，tanθ=O.75，g取10m/s²。求：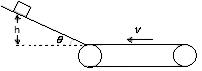

（1）物体第一次滑到底端的速度大小。
（2）从滑上传送带到第一次离开传送带的过程中，求传送带对物体所做功及物体对传送带做功。
（3）从物体开始下滑到最终停在斜面底端，物体在斜面上通过的总路程。

某水上游乐场举办了一场趣味水上比赛．如图所示，质量m=60kg的参赛者（可视为质点），在河岸上A点双手紧握一根长L=5.0m的不可伸长的轻绳，轻绳另一端系在距离水面高H=10.0m的O点，此时轻绳与竖直方向的夹角为θ=37°，C点是位于O点正下方水面上的一点，距离C点x=5.0m处的D点固定着一只救生圈，O、A、C、D各点均在同一竖直面内，若参赛者双手抓紧绳端点，从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出，当摆到O点正下方的B点时松开手，此后恰能落在救生圈内。（sin37°=0.6，cos37°=0.8， g=10m/s²）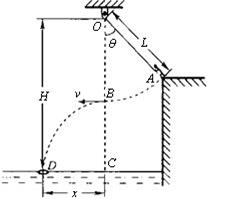

（1）求参赛者经过B点时速度的大小v；
（2）求参赛者从台阶上A点跃出时的动能E_K；
（3）若手与绳之间的动摩擦因数为0.6，参赛者要顺利完成比赛，则每只手对绳的最大握力不得小于多少？（设最大静摩擦等于滑动摩擦力）

试卷网试题网古诗词网作文网范文网