由三颗星体构成的系统,忽略其他星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心
在三角形所在的平面内做相同角速度的圆周运动(图示为
、
、
三颗星体质量不相同时的一般情况)。若A星体质量为
,
、
两星体的质量均为
,三角形边长为
。求:

(1) 星体所受合力大小 ;
(2)
星体所受合力大小
;
(3)
星体的轨道半径
;
(4)三星体做圆周运动的周期
。
如图所示,一带电平行板电容器水平放置,金属板M上开有一小孔.有A、B、C三个质量均为m、电荷量均为+q的带电小球(可视为质点),其间用长为L的绝缘轻杆相连,处于竖直状态.已知M、N两板间距为3L,现使A小球恰好位于小孔中,由静止释放并让三个带电小球保持竖直下落,当A球到达N极板时速度刚好为零,求:
⑴三个小球从静止开始运动到A球刚好到达N板的过程中,重力势能的减少量;
⑵两极板间的电压;
⑶小球在运动过程中的最大速率.
如图所示,在竖直向下的匀强电场中,一个质量为m带负电的小球从斜轨道上的A点由静止滑下,小球通过半径为R的圆轨道顶端的B点时恰好不落下来。已知轨道是光滑而又绝缘的,且小球的重力是它所受的电场力2倍。求:
(1)A点在斜轨道上的高度h为多少?
(2)小球运动到最低点时对轨道的最小压力为多少?
如图所示,在倾角为θ=30°的斜面上,固定一宽L=0.25 m的平行金属导轨,在导轨上端接入电源和滑动变阻器R.电源电动势E=12 V,内阻r=1 Ω,一质量m=20 g的金属棒ab与两导轨垂直并接触良好.整个装置处于磁感应强度B=0.80 T、垂直于斜面向上的匀强磁场中(导轨与金属棒的电阻不计).金属导轨是光滑的,取g=10 m/s2,要保持金属棒在导轨上静止,求:
(1)通过金属棒的电流;
(2)滑动变阻器R接入电路中的阻值.
如图所示, A、B、C、D为固定于竖直平面内的闭合绝缘轨道,AB段、CD段均为半径R=2.5m的半圆,BC、AD段水平,AD ="BC" =" 8" m,B、C之间的区域存在水平向右的有界匀强电场场强E= 6 ×105 V/m;质量为m = 4×10-3 kg、带电量q = +1×10-8C的小环套在轨道上,小环与轨道AD段之间存在摩擦且动摩擦因数处处相同,小环与轨道其余部分的摩擦忽略不计,现使小环在D点获得某一初速度沿轨道向左运动,若小环在轨道上可以无限循环运动,且小环每次到达圆弧上的A点时,对圆轨道刚好均无压力.求: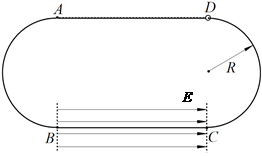
(1)小环通过A点时的速度多大;
(2)小环与AD段间的动摩擦因数μ;
(3)小环运动到D点时的速度多大.
在半径R=4000 km的某星球表面,宇航员做了如下实验,实验装置如图甲所示,竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量m=0.2 kg的小球从轨道上高H处的某点由静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙所示,忽略星球自转.

求:(1)圆弧轨道BC的半径r;
(2)该星球的第一宇宙速度vⅠ.