(本小题满分7分) 选修4—4:极坐标与参数方程
已知曲线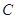 的极坐标方程是
的极坐标方程是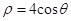 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是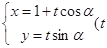 是参数
是参数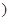 .
.
(Ⅰ)写出曲线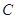 的参数方程;
的参数方程;
(Ⅱ)若直线 与曲线
与曲线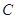 相交于
相交于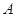 、
、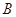 两点,且
两点,且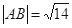 ,求直线
,求直线 的倾斜角
的倾斜角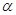 的值.
的值.
某学校篮球队、羽毛球队、乒乓球队的某些队员不止参加了一支球队,具体情况如图所示,现从中随机抽取一名队员,求:
(1)该队员只属于一支球队的概率;
(2)该队员最多属于两支球队的概率.
甲、乙两人做出拳游戏(锤子、剪刀、布),锤子记为“⊥”,剪刀记为“×”,布记为“□”
求:(1)列出实验所有可能的结果(2)平局的概率;(3)甲赢的概率;
样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计: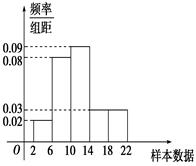
(1)求样本数据落在[6,10)内的频数.
(2)求数据落在[2,10)内的概率
选择合适的抽样方法抽样,并写出抽样过程.
(1)有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取3个;
(2)有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个;
(3)有甲厂生产的300个篮球,抽取10个;
(4)有甲厂生产的300个篮球,抽取30个.
设有120件产品,其中一级品有24件,二级品有36件,三级品有60件,用分层抽样法从中抽取一个容量为20的样本.试说明这种抽样方法是公平的.