(本小题满分7分) 选修4—5:不等式选讲
已知关于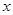 的不等式:
的不等式: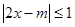 的整数解有且仅有一个值为2.
的整数解有且仅有一个值为2.
(Ⅰ)求整数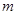 的值;
的值;
(Ⅱ)已知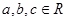 ,若
,若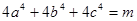 ,求
,求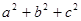 的最大值.
的最大值.
(本小题满分13分)函数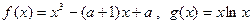 .
.
(Ⅰ)若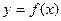 ,
, 在
在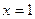 处的切线相互垂直,求这两个切线方程;
处的切线相互垂直,求这两个切线方程;
(Ⅱ)若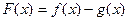 单调递增,求
单调递增,求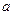 的取值范围.
的取值范围.
(本小题满分13分)已知幂函数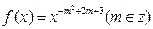 为偶函数,且在区间
为偶函数,且在区间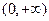 上是单调增函数.
上是单调增函数.
(Ⅰ)求函数
 的解析式;
的解析式;
(Ⅱ)设函数 ,其中
,其中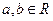 .若函数
.若函数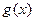 仅在
仅在
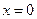 处有极值,求
处有极值,求 的取值范围.
的取值范围.
(本小题满分13分)已知函数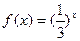 ,函数
,函数 是函数
是函数 的反
的反 函数.
函数.
(Ⅰ)若函数 的定义域为R,求实数
的定义域为R,求实数 的取值范围;
的取值范围;
(Ⅱ)当x∈[-1,1]时,求函数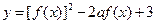 的最小值
的最小值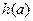 .
.
(本小题满分12分)已知定义域为R的函数 是奇函数.
是奇函数.
(Ⅰ)求 a的值,并指出函数
a的值,并指出函数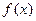 的单调性(不必说明单调性理
的单调性(不必说明单调性理 由);
由);
(Ⅱ)若对任意的 ,不等式
,不等式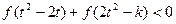 恒成立,求
恒成立,求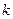 的取值范围.
的取值范围.
已知函数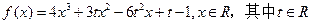 ,
,
(1)当t=1时,求曲线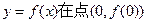 处的切线方程;
处的切线方程;
(2)当t≠0时,求的单调区间;
(3)证明:对任意的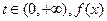 在区间(0,1)内均存在零点。
在区间(0,1)内均存在零点。