（1）如图1，在△ABC中，∠ABC的平分线BF交AC于F，过点F作DF∥BC，求证：BD=DF．
（2）如图2，在△ABC中，∠ABC的平分线BF与∠A CB的平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E．那么BD，CE，DE之间存在什么关系 ？并证明这种关系．
（3）如图3，在△ ABC中，∠ABC的平分线BF与∠ACB的外角平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E．那么BD，CE，DE之间存在什么关系？请写出你的猜想．（不需证明）
某商场为了吸引顾客，设计了一种促销活动：在一个不透明的箱子里放有4个小球，球上分别标有“0元”、 “10元”、“20元”和“30元”的字样.规定；顾客在本商场同一日内，每消费200元就可以在箱子里先后摸出两个球（第一次摸出后不放回），商场根据两小球所标金额的和返还相应金额的购物券，可以重新在本商场消费.某顾客刚好消费200元.
（1）该顾客至少可得到（）元购物券，至多可以得到（）元购物券
（2）请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于30元的概率
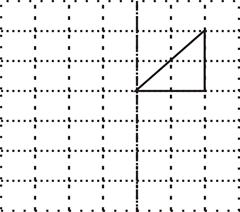
如图为7×7的正方形网格,
（1）作出等腰直角三角形ABC关于直线MN成轴对称变换的像⊿A1BC1（A对应A1，C对应C1）；
（2）作出⊿A1BC1绕点B逆时针旋转90o得到的像⊿A2BC2(A1对应A2, C1对应C2)；
（3）填空：⊿A2BC2可以看作将⊿ABC经过连续两次平移得到,则这两次平移具体的操作方法是 _________________________________________________________（需指明每次平移的方向和距离）.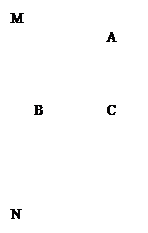
解方程（组）：
(1) 
(2)
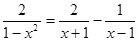
因式分解：
（1）
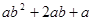
（2）
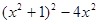
先化简
，然后从 0，-1，1，2，-2中取一个合适的数作为
的值代入