如图,在Rt△ACB中,∠C=90°, AC=6m,BC=8m,点P、Q同时由A、B两点出发分别沿AC,BC方向向点C匀速运动,它们的速度都是1m/s,几秒后△PCQ的面积为Rt△ACB面积的一半?
将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长做成一个正方形.
(1)要使这两个正方形的面积之和等于 ,那么这段铁丝剪成两段后的长度分别是多少?
,那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于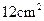 吗?若能,求出两段铁丝的长度;若不能,请说明理由.
吗?若能,求出两段铁丝的长度;若不能,请说明理由.
如图,已知一次函数y=kx +b的图象与反比例函数
+b的图象与反比例函数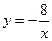
的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2.
求:(1)一次函数的解析式;
(2)△ABC的面积.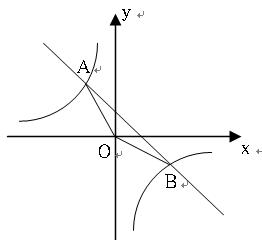
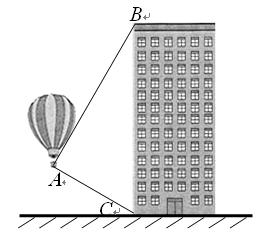
如图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角
为 ,看这栋高楼底部的俯角为
,看这栋高楼底部的俯角为 ,热气球与高楼的水平距离为60 m,这栋高楼有多
,热气球与高楼的水平距离为60 m,这栋高楼有多
高?(结果精确到0.1 m,参考数据: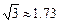 )
)
欢欢有红色、白色、黄色三件上衣,又有米色、白色的两条裤子.
(1)她随机拿出一件上衣和一条裤子,用树状图(或列表法)表示所有可能出现的结果;
(2)如果欢欢最喜欢的穿着搭配是白色上衣配米色裤子,求欢欢随机拿出一件上衣和一条裤子正好是她最喜欢的穿着搭配的概率.
如图, F、C是线段AD上的两点,AB∥DE,BC∥EF ,AF=DC,
,AF=DC,
连结AE、BD,求证:四 边形ABDE是平行四边形。
边形ABDE是平行四边形。