﹣(本题12分)在一平直河岸 同侧有
同侧有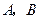 两个村庄,
两个村庄,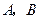 到
到 的距离分别是3km和2km,
的距离分别是3km和2km,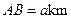
 .现计划在河岸
.现计划在河岸 上建一抽水站
上建一抽水站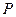 ,用输水管向两个村庄供水.
,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图(1)是方案一的示意图,设该方案中管道长度为 ,且
,且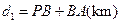 (其中
(其中 于点
于点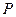 );图(2)是方案二的示意图,设该方案中管道长度为
);图(2)是方案二的示意图,设该方案中管道长度为 ,且
,且 (其中点
(其中点 与点
与点 关于
关于 对称,
对称, 与
与 交于点
交于点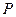 ).
).
 |
(1)观察计算
在方案一中,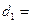 km(用含
km(用含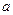 的式子表示);
的式子表示);
在方案二中,组长小宇为了计算 的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算,
的长,作了如图(3)所示的辅助线,请你按小宇同学的思路计算, km(用含
km(用含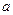 的式子表示).
的式子表示).
(2)探索归纳
①当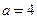 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”);
当 时,比较大小:
时,比较大小: (填“>”、“=”或“<”);
(填“>”、“=”或“<”); ②请你参考右边方框中的方法指导,
②请你参考右边方框中的方法指导,
就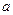 (当
(当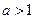 时)的所有取值情况进
时)的所有取值情况进
行分析,要使铺设的管道长度较短,
应选择方案一还是方案二?
(年贵州省遵义市)某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本 (万元/吨)与产量
(万元/吨)与产量 (吨)之间是一次函数关系,函数
(吨)之间是一次函数关系,函数 与自变量
与自变量 的部分对应值如下表:
的部分对应值如下表:
 (吨) (吨) |
10 |
20 |
30 |
 (万元/吨) (万元/吨) |
45 |
40 |
35 |
(1)求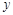 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
(3)市场调查发现,这种产品每月销售量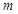 (吨)与销售单价
(吨)与销售单价 (万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
(万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)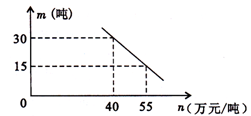
(年贵州省黔东南州)如图,已知二次函数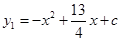 的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为
的图象与x轴的一个交点为A(4,0),与y轴的交点为B,过A、B的直线为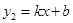 .
.
(1)求二次函数 的解析式及点B的坐标;
的解析式及点B的坐标;
(2)由图象写出满足 的自变量x的取值范围;
的自变量x的取值范围;
(3)在两坐标轴上是否存在点P,使得△ABP是以AB为底边的等腰三角形?若存在,求出P的坐标;若不存在,说明理由.
(年青海省中考)如图,二次函数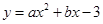 的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.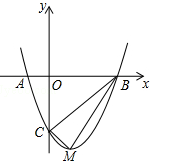
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(年青海省中考)某玩具商计划生产A、B两种型号的玩具投入市场,初期计划生产100件,生产投入资金不少于22400元,但不超过22500元,且资金要全部投入到生产这两种型号的玩具.假设生产的这两种型号玩具能全部售出,这两种玩具的生产成本和售价如表:
(1)该玩具商对这两种型号玩具有哪几种生产方案?
(2)该玩具商如何生产,就能获得最大利润?
(年新疆、生产建设兵团)如图,直线 与x轴、y轴分别交于点A、B.抛物线
与x轴、y轴分别交于点A、B.抛物线 经过A、B,并与x轴交于另一点C,其顶点为P,
经过A、B,并与x轴交于另一点C,其顶点为P,
(1)求a,k的值;
(2)在图中求一点Q,A.B、C为顶点的四边形是平行四边形,请直接写出相应的点Q的坐标;
(3)抛物线的对称轴上是否存在一点M,使△ABM的周长最小?若存在,求△ABM的周长;若不存在,请说明理由;
(4)抛物线的对称轴是上是否存在一点N,使△ABN是以AB为斜边的直角三角形?若存在,求出N点的坐标,若不存在,请说明理由.