(本题10分)2013年第23号台风“菲特”给浙江省带来了严重的影响。强降雨导致多处河水猛涨,城区受淹。西湖也出现了罕见的水满现象。在10月7日凌晨,西湖达到警戒水位7.3 m .下表记录了这几日西湖水位的变化情况:(把10月7日凌晨的水位记作0,此后,正数表示比前一观察时间上升,负数表示下降)。
| 时间 |
10月7日凌晨 |
10月7日15时 |
10月8日、 |
10月9日 8时 |
10月10日12时 |
10月10日15点 |
| 水位变化 (米) |
0 |
+0.15 |
+0.20 |
-0.13 |
-0.26 |
-0.03 |
(1)10月9日8时西湖水位是多少?
(2)这几日西湖水位最高值是多少?超过警戒水位多少米?
(3)从表中可以得知什么时候开始西湖水位已恢复到警戒水位之下?
根据下列事件发生的可能性,把A、B、C、D、E填入事件后的括号里.
1.3个人下棋,必定有一个是旁观者.()
2.任意一张扑克牌,一定是红桃.()
3.白天一定能见到太阳.()
4.你能举起300公斤的重物.()
5.任意抓一把围棋子,个数是奇数.()
A不可能发生 B发生的可能性小于50%
C发生的可能性大于50% D必然发生100%
E发生的可能性等于50%
下图是上海市区及县土地面积变化图,其中细线表示市区,粗线表示县。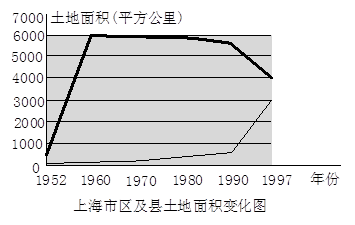
(1)从1952~1960年,上海市郊县面积大约扩大了多少平方公里?1960 年的上海市郊县面积是1952年的上海市郊县面积的多少倍?
(2)1960~1980年间,上海市区及郊县土地面积的变化情况如何? 说明什么问题?
(3)从图中可以发现,从1980年开始,上海市区土地面积越来越大, 而上海市郊县面积却越来越小,这说明什么问题?1980年以后,上海市区及郊县的土地总面积的变化情况如何?这又说明什么问题?
某人射击10发子弹,情况如表:
| 射击次序 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 中环数(环) |
6 |
8 |
8 |
7 |
8 |
9 |
10 |
8 |
9 |
10 |
(1)从表中可得到什么信息。
(2)此人的平均数成绩是每发多少环?(保留1个有效数字)
(3)用折线统计图表示出来.
下表是某职工在1996~2001年生活开支的变化情况:
| 年份 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
| 家庭实用型生活消费(元) |
7200 |
7150 |
7000 |
7000 |
6900 |
6830 |
| 健康保健品消费(元) |
430 |
340 |
580 |
640 |
1560 |
1790 |
| 旅游性消费(元) |
870 |
890 |
940 |
1350 |
1400 |
2100 |
(1)从表中能得到什么信息?
(2)每年的总消费数是增加了,还是减少了?
(3)画折线统计图表示表中的数据。
下面是近年来国内生产总值年增长率的变化统计表:
| 年份 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
| 生产总值年增长率(%) |
12.6 |
105 |
9.6 |
8.8 |
7.8 |
7.1 |
8.0 |
(1)用一幅折线统计图表示国内生产总值年增长率的变化情况;
(2)将上面的数据制成形象生动的统计图;
(3)如果要利用面积分别表示五年的生产总值年增长率,t年的生产总值年增长率的面积之比大约是多少?
(4)哪一年国内生产总值的年增长率开始回升?