王强在一次高尔夫球的练习中，在某处击球，其飞行路线满足抛物线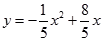
，其中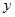
（m）是球的飞行高度，
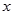（m）是球飞出的水平距离，结果球离球洞的水平距离还有2m．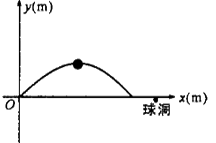
（1）请写出抛物线的开口方向、顶点坐标、对称轴．
（2）请求出球飞行的最大水平距离．
（3）若王强再一次从此处击球，要想让球飞行的最大高度不变且球刚好进洞，则球飞行路线应满足怎样的抛物线，求出其解析式．
化简：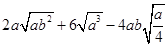
计算：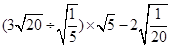
在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN⊥DM，垂足为M，交∠CBE的平分线于点N .
（1）写出点C的坐标；
（2）求证：MD = MN；
（3）连接DN交BC于点F，连接FM，下列两个结论：①FM的长度不变；②MN平分∠FMB，其中只有一个结论是正确的，请你指出正确的结论，并给出证明.
已知：在四边形ABCD中，AC = BD，AC与BD交于点O，∠DOC = 60°.
（1）当四边形ABCD是平行四边形时（如图1），证明AB + CD = AC；
（2）当四边形ABCD是梯形时（如图2），AB∥CD，线段AB、CD和线段AC之间的数量关系是____；
（3）如图3，四边形ABCD中，AB与CD不平行，结论AB + CD = AC是否仍然成立？如果成立，请给予证明；如果不成立，请说明理由.
若正整数a、b、c满足方程a2+b2=c2 ,则称这一组正整数（a、b、c）为“商高数”，下面列举五组“商高数”：（3，4，5），（5，12，13），（6，8，10），（7，24，25），（12，16，20），注意这五组“商高数”的结构有如下规律：
根据以上规律，回答以下问题：
（1）商高数的三个数中，有几个偶数，几个奇数？
（2）写出各数都大于30的两组商高数。
（3）用两个正整数m、n（m＞n）表示一组商高数，并证明你的结论。