(文科)在平面直角坐标系xOy中,点P到点F(3,0)的距离的4倍与它到直线x=2的距离的3倍之和记为d,当P点运动时,d恒等于点P的横坐标与18之和
(Ⅰ)求点P的轨迹C;
(Ⅱ)设过点F的直线I与轨迹C相交于M,N两点,求线段MN长度的最大值。
(本小题12分)某中学在高一开设了4门选修课,每个学生必须且只需选修1门选修课,对于该年级的甲、乙、丙3名学生,回答下列问题。(I)求这3名学生选择的选修课互不相同的概率;(II)求恰有2门选修课没有被这3名学生选择的概率;(III)某一选修课被这3名学生选择的人数的数学期望。
(本小题10分)已知向量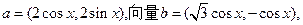
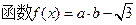 (1)求函数
(1)求函数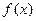 的最小正周期;(2)求函数
的最小正周期;(2)求函数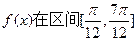 上的值域。
上的值域。
【理科】已知函数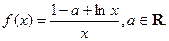
(I)求 的极值;
的极值;
(II)若 的取值范围;
的取值范围;
(III)已知
(本小题满分14分)已知数列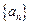 中,
中, ,
, ,其前
,其前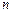 项和
项和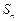 满足
满足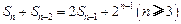 .令
.令 .
.
(Ⅰ)求数列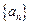 的通项公式;
的通项公式;
(Ⅱ)若 ,求证:
,求证: (
(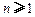 );
);
(Ⅲ)令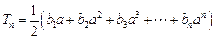 (
( ),求同时满足下列两个条件的所有
),求同时满足下列两个条件的所有 的值:①对于任意正整数
的值:①对于任意正整数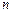 ,都有
,都有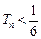 ;②对于任意的
;②对于任意的 ,均存在
,均存在 ,使得
,使得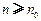 时,
时,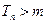 .
.
(本小题满分16分)函数 其中
其中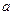 为常数,且函数
为常数,且函数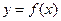 和
和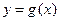 的图像在其与坐标轴的交点处的切线互相平行
的图像在其与坐标轴的交点处的切线互相平行
(1)、求函数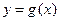 的解析式
的解析式
(2)、若关于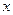 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。