(理科)已知中心在原点,焦点在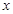 轴上的椭圆
轴上的椭圆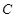 过点
过点 ,离心率为
,离心率为 ,点
,点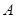 为其右顶点.过点
为其右顶点.过点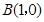 作直线
作直线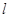 与椭圆
与椭圆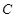 相交于
相交于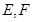 两点,直线
两点,直线 ,
,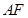 与直线
与直线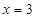 分别交于点
分别交于点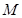 ,
, .
.
(Ⅰ)求椭圆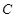 的方程;
的方程;
(Ⅱ)求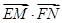 的取值范围.
的取值范围.
已知等差数列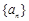 的前
的前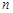 项和为
项和为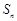 ,
,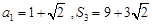
(1)求数列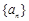 的通项公式
的通项公式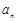 与前
与前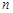 项和
项和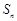 ;
;
(2)设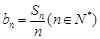 求证:数列
求证:数列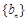 中任意不同的三项都不可能成为等比数列
中任意不同的三项都不可能成为等比数列
如图,四棱锥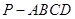 中,底面
中,底面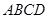 是
是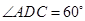 的菱形,
的菱形,
侧面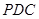 是边长为2的正三角形,且与底面
是边长为2的正三角形,且与底面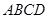 垂直,
垂直,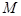 为
为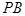 的中点.
的中点.
(1)求证: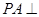 平面
平面 ;
;
(2)求二面角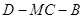 的余弦值.
的余弦值.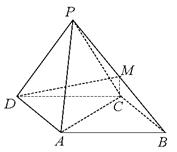
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为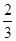 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1) 随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为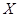 ,求
,求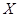 的数学期望;
的数学期望;
(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
已知函数f(x)= sin2x+sinxcosx-
sin2x+sinxcosx- (xÎR).
(xÎR).
(1)若 ,求f(x)的最大值;
,求f(x)的最大值;
(2)在△ABC中,若A<B,f(A)=f(B)= ,求
,求  的值.
的值.
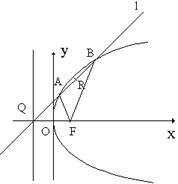
如图,F是抛物线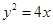 的焦点,Q是准线与x轴的交点,直线
的焦点,Q是准线与x轴的交点,直线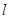 经过点Q。
经过点Q。
(Ⅰ)直线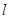 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求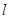 方程;
方程;
(Ⅱ)直线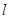 与抛物线交于A、B两点;
与抛物线交于A、B两点;
(i)设FA、FB的斜率分别为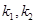 ,求
,求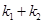 的值;
的值;
(ii)若点R在线段AB上,且满足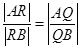 ,求点R的轨迹方程。
,求点R的轨迹方程。