函数y＝sin（x－
）cosx的最小值是 .
已知F1、F2是椭圆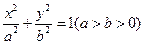
的左、右焦点，A是椭圆上位于第一象限内的一点，点B也在椭圆上，且满足
（
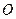是坐标原点），
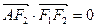,若椭圆的离心率等于
.
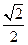（1）求直线AB的方程；
（2）若三角形ABF2的面积等于4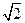
，求椭圆的方程；
（3）在（2）的条件下，椭圆上是否存在点M，使得三角形MAB的面积等于8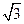
.
已知函数f(x)=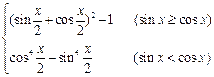 
（1）画出f(x)在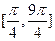
上的图象，并写出x∈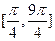上的单调区间；
（2）若x∈R，判断f(x)是否为周期函数。如果是，求出最小正周期。
已知某单位有50名职工，现要从中抽取
10名职工，将全体职工随机按1~50编号，并
号顺序平均分成10组，按各组内抽按编取的
编号依次增加5进行系统抽样。
（1）若第5组抽出的号码为22，写出
所有被抽出职工的号码；
（2）分别统计这10名职工的体重（单
位：公斤），获得体重数据的茎叶图如图所
示，求该样本的方差；
（3）在（2）的条件下，从这10名职工中随机抽取两名体重不轻于73公斤（
73公斤）的职工，求被抽取到两名职工体重之和大于等于154公斤的概率。
设n阶方阵
任取A n中的一个元素，记为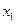
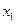；划去所在行与列，将剩下的元素按原来的位置关系组成n-1阶方阵An-1，任取A n-1中一个元素，记为
，划去所在行与列，……将最后剩下的一个元素记为
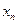，记
，
若n=3时，则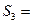
，若n=k时，则
。
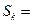如图，测量河对岸的塔高
时，可以选与塔底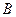
在
同一水平面内的两个测点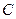
与
．测得∠BCD＝15°，
∠BDC＝30°，CD＝30米，并在点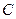测得塔顶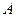
的仰角为60°,则塔高AB=米。