如图所示四棱锥 中,
中,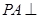 底面
底面 ,四边形
,四边形 中,
中,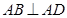 ,
,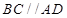 ,
, ,
,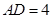 .
.
(1)求四棱锥 的体积;
的体积;
(2)求证: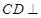 平面
平面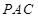 ;
;
(3)在棱 上是否存在点
上是否存在点 (异于点
(异于点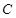 ),使得
),使得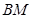 ∥平面
∥平面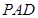 ,若存在,求
,若存在,求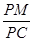 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知数列{an}的前n项和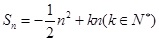 ,且Sn的最大值为8.
,且Sn的最大值为8.
(1)确定常数k,求an;
(2)求数列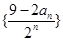 的前n项和Tn。
的前n项和Tn。
已知函数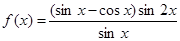 。
。
(1)求 的定义域及最小正周期;
的定义域及最小正周期;
(2)求 的单调递增区间。
的单调递增区间。
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列;
(Ⅱ)求X的数学期望E(X).
已知定义域为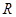 的函数
的函数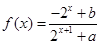 是奇函数。
是奇函数。
(Ⅰ)求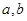 的值;
的值;
(Ⅱ)若对任意的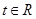 ,不等式
,不等式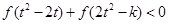 恒成立,求
恒成立,求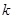 的取值范围;
的取值范围;
已知数列 中,
中,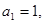 且点
且点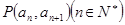 在直线
在直线 上。
上。
(1)求数列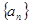 的通项公式;
的通项公式; (2)
(2) 求函数
求函数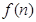 的最小值;
的最小值;
(3)设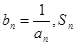 表示数列
表示数列 的前
的前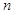 项和。试问:是否存在关于
项和。试问:是否存在关于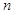 的整式
的整式 ,使得
,使得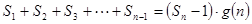 对于一切不小于2的自然数
对于一切不小于2的自然数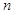 恒成立?若存在,写出
恒成立?若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。