△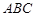 中,角
中,角 的对边分别为
的对边分别为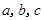 ,且
,且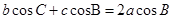 .
.
(1)求角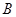 的大小;
的大小;
(2)若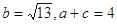 ,求△
,求△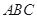 的面积.
的面积.
已知函数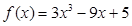 .
.
(Ⅰ)求函数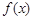 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数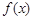 在
在 的最大值和最小值.
的最大值和最小值.
求下列函数的导数.
(Ⅰ) (Ⅱ)
(Ⅱ)
(Ⅲ)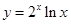 (Ⅳ)
(Ⅳ)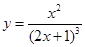 .
.
定义在 上的函数
上的函数 ,对于任意的m,n∈(0,+∞),都有
,对于任意的m,n∈(0,+∞),都有 成立,当x>1时,
成立,当x>1时, .
.
(1)求证:1是函数 的零点;
的零点;
(2)求证: 是(0,+∞)上的减函数;
是(0,+∞)上的减函数;
(3)当 时,解不等式
时,解不等式 .
.
已知向量a=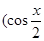
 ,b=
,b=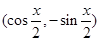 ,c=
,c= ,
,
(1)求证:(a+b)⊥(a-b);
(2)设函数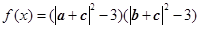
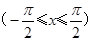 ,求
,求 的最大值和最小值.[来
的最大值和最小值.[来
正在建设中的长春地铁一号线将大大缓解市内南北交通的压力. 根据测算,如果一列车每次拖4节车厢,每天能来回16次;如果每次拖7节车厢,则每天能来回10次;每天来回次数是每次拖挂车厢节数的一次函数,每节车厢单向一次最多能载客110人,试问每次应拖挂多少节车厢才能使该列车每天营运人数最多?并求出每天最多的营运人数.(注:营运人数指列车运送的人数) .