解不等式
已知等差数列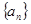 满足:
满足: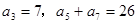 ,
, 的前
的前 项和为
项和为 .
.
(1)求 及
及 ;
;
(2)令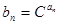 (其中
(其中 为常数,且
为常数,且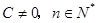 ),求证数列
),求证数列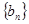 为等比数列.
为等比数列.
设函数 ,
,
(1)若不等式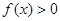 的解集
的解集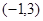 .求
.求 的值;
的值;
(2)若 求
求 的最小值.
的最小值.
设数列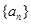 的前
的前 项和为
项和为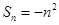 ,数列
,数列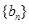 满足:
满足: ,已知
,已知 对任意
对任意 都成立
都成立
(1)求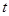 的值
的值
(2)设数列 的前
的前 项的和为
项的和为 ,问是否存在互不相等的正整数
,问是否存在互不相等的正整数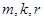 ,使得
,使得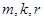 成等差数列,且
成等差数列,且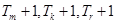 成等比数列?若存在,求出
成等比数列?若存在,求出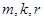 ;若不存在,说明理由
;若不存在,说明理由
某渔业公司年初用49万元购买一艘捕鱼船,第一年各种费用6万元,以后每年都增加2万元,每年捕鱼收益25万元.
(1)问第几年开始获利?
(2)若干年后,有两种处理方案:①年平均获利最大时,以18万元出售该渔船;②总纯收入获利最大时,以9万元出售该渔船.问哪种方案最合算?
在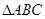 中,角
中,角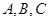 的对边分别为
的对边分别为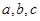 ,且
,且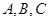 成等差数列
成等差数列
(1)若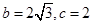 ,求
,求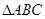 的面积
的面积
(2)若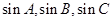 成等比数列,试判断
成等比数列,试判断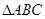 的形状
的形状