(本小题满分13分)已知函数 (其中
(其中 ,
, 是自然对数的底数,
是自然对数的底数,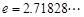 ).
).
(Ⅰ)当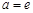 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)求证:对任意正整数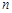 ,都有
,都有 .
.
如图,在棱长为2的正方体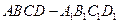 中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
中,E是BC1的中点.求直线DE与平面ABCD所成角的大小(结果用反三角函数值表示).
已知圆:x2+y2-4x-6y+12=0,(1)求过点 的圆的切线方程;
的圆的切线方程;
(2)点 为圆上任意一点,求
为圆上任意一点,求 的最值。
的最值。
在四棱锥 中,
中, ,
, ,且DB平分
,且DB平分 ,E为PC的中点,
,E为PC的中点, ,
, PD=3,(1)证明
PD=3,(1)证明 (2)证明
(2)证明
(3)求四棱锥 的体积。
的体积。
有一个公益广告说:“若不注意节约用水,那么若干年后,最有一滴水只能是我们的眼泪。”我国是水资源匮乏的国家。为鼓励节约用水,某市打算出台一项水费政策措施,规定:每一季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分的水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%。设某人本季度实际用水量为 吨,应交水费为f(x),(1)求
吨,应交水费为f(x),(1)求 的值;(2)试求出函数f(x)的解析式。
的值;(2)试求出函数f(x)的解析式。
过点 的直线l将圆
的直线l将圆 分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。
分成两段弧,当劣弧所对的圆心角最小时,求直线l的斜率。