设函数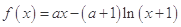 ,其中
,其中 .
.
(1)当 时,证明不等式
时,证明不等式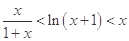 ;
;
(2)设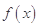 的最小值为
的最小值为 ,证明
,证明 .
.
(本小题满分12分 ) 如图,在正方体
) 如图,在正方体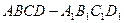 中,
中,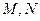 分别为棱
分别为棱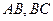 的中点.
的中点.
(1)试判截面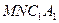 的形状,并说明理由;
的形状,并说明理由;
(2)证明:平面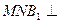 平面
平面 .
.
某项竞赛分别为初赛、复 赛、决
赛、决 赛三个阶段进行,每个阶段选手要
赛三个阶段进行,每个阶段选手要
回答一个问题.规定正确回答问题者进入下一阶段竞赛,否则即遭淘汰.已知某选手通过初赛、复赛、决赛的概率分别是 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(1)求该选手在复赛阶段被淘汰的概率;
(2)设该选手在竞赛中回答问题的个数为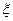 ,求
,求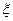 的分布列、数学期望和方差.
的分布列、数学期望和方差.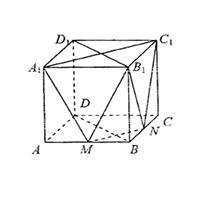
已知 ,且
,且 .
.
(1)求实数 的值;
的值;
(2)求函数 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)
直三棱柱ABO-A1B1O1中,∠AOB=90°,D为AB的中点,AO=BO=BB1=2.
①求证:BO1⊥AB1;
②求证:BO1∥平面OA1D;
③求三棱锥B—A1OD的体积。
(本小题满分12分)
甲、乙两人独立地破译一份密码,甲能破译出密码的概率是1/3,乙能破译出密码的概率是1/4,试求:
①甲、乙两人都译不出密码的概率;
②甲、乙两人中恰有一人能译出密码的概率;
③甲、乙两人中至多有一人能译出密码的概率.