为选拔选手参加“中国汉字听写大会”，某中学举行了一次“汉字听写大赛”活动．为了了解本次竞赛学生的成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为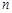
）进行统计．按照
，
，
，
，
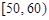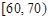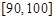的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在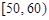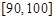，的数据）．
（1）求样本容量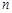和频率分布直方图中的
、
的值；
（2）在选取的样本中，从竞赛成绩在80分以上（含80分）的学生中随机抽取3名学生参加“中国汉字听写大会”，设随机变量
表示所抽取的3名学生中得分在内的学生人数，求随机变量的分布列及数学期望．
如图四棱锥P-ABCD中，底面ABCD为矩形，PA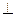
底面ABCD，PA=AB=
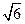，点E是棱PB的中点。（1）求直线AD与平面PBC的距离。
（2）若AD=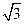
，求二面角A-EC-D的平面角的余弦值。
甲、乙两人独立解出某一道数学题的概率相同。已知该题被甲或乙解出的概率为0.36。求：（I）甲独立解出该题的概率。（II）恰有1人解出该题的概率。
已知函数
（1）写出
的单调区间；（2）设
在[0，
]上的最大值。
已知全集
集合
，
，求
(本题满分12分)已知函数f(x) =4x3+ax2+bx＋5在x=－1与x=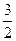
处有极值。
(1)写出函数的解析式；
(2)求出函数的单调区间；
(3)求f(x)在[-1,2]上的最值。