(本小题满分12分)已知函数 的图像过点
的图像过点 .
.
(1)求 的值;
的值;
(2)将函数 图像上各点的横坐标变为原来的2倍,纵坐标不变,得到函数
图像上各点的横坐标变为原来的2倍,纵坐标不变,得到函数 的图像,求函数
的图像,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
已知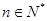 ,且
,且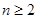 ,求证:
,求证: .
.
已知定义在正实数集上的函数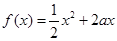 ,
, ,其中
,其中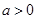 .设两曲线
.设两曲线 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用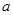 表示
表示 ,并求
,并求 的最大值;
的最大值;
(2)判断当 时,
时,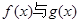 的大小,并证明.
的大小,并证明.
(Ⅰ)小问5分,(Ⅱ)小问7分)
安排四个大学生到A、B、C三个学校支教,设每个大学生去任何一个学校是等可能的.
(1)求四个大学生中恰有两人去A校支教的概率.
(2)设有大学生去支教的学校的个数为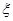 ,求
,求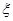 的分布列.
的分布列.
探究:是否存在常数a、b、c使得等式1·22+2·32+…+n(n+1)2=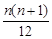 (an2+bn+c)
(an2+bn+c)
对对一切正自然数n均成立,若存在求出a、b、c,并证明;若不存在,请说明理由.
已知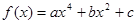 的图象经过点
的图象经过点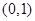 ,且在
,且在 处的切线方程是
处的切线方程是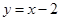
(1)求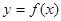 的解析式;
的解析式;
(2)求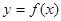 的单调递增区间
的单调递增区间