（2013高考真题）抛物线y2＝4x的焦点到双曲线x2－
＝1的渐近线的距离是（）
A． |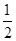
B． |
C．1 | D． |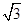
已知直线l过抛物线C的焦点，且与C的对称轴垂直，l与C交于A，B两点，|AB|＝12，P为C的准线上一点，则△ABP的面积为（）
| A．18 | B．24 | C．36 | D．48 |
设P是双曲线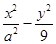
＝1上一点，双曲线的一条渐近线方程为3x－2y＝0，F1，F2分别是双曲线的左，右焦点，若|PF1|＝3，则|PF2|＝（）
| A．1或5 | B．6 | C．7 | D．9 |
椭圆
＝1（a＞b＞0）的两顶点为A（a,0），B（0，b），且左焦点为F，△FAB是以角B为直角的直角三角形，则椭圆的离心率e为（）
A． |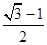
B． |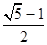
C． |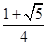
D． |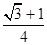
以坐标轴为对称轴，原点为顶点且过圆x2＋y2－2x＋6y＋9＝0圆心的抛物线方程是（）
| A．y＝3x2或y＝－3x2 |
| B．y＝3x2 |
| C．y2＝－9x或y＝3x2 |
| D．y＝－3x2或y2＝9x |
，
的最小正周期为
，且
，则（ ）
，
，