某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1张卡片
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的.
如图, 已知直线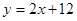 分别与
分别与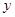 轴,
轴, 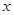 轴交于
轴交于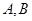 两点, 点
两点, 点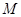 在
在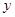 轴上. 以点
轴上. 以点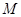 为圆心的⊙
为圆心的⊙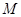 与直线
与直线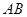 相切于点
相切于点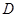 , 连接
, 连接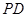 .
.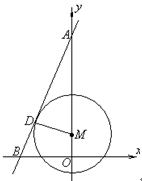
(1) 求证:  ∽
∽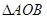 ;
;
(2)如果⊙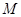 的半径为
的半径为 , 求出点
, 求出点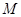 的坐标, 并写出以
的坐标, 并写出以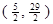 为顶点, 且过点
为顶点, 且过点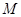 的抛物线的解析式;
的抛物线的解析式;
(3) 在(2)的条件下, 在此抛物线上是否存在点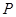 , 使得以
, 使得以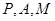 三点为顶点的三角形与
三点为顶点的三角形与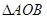 相似? 如果存在, 请求出所有符合条件的点
相似? 如果存在, 请求出所有符合条件的点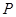 的坐标; 如果不存在, 请说明理由.
的坐标; 如果不存在, 请说明理由.
在平面直角坐标中,边长为2的正方形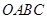 的两顶点
的两顶点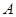 、
、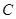 分别在
分别在 轴、
轴、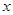 轴的正半轴上,点
轴的正半轴上,点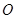 在原点.现将正方形
在原点.现将正方形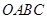 绕
绕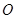 点顺时针旋转,当
点顺时针旋转,当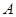 点第一次落在直线
点第一次落在直线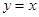 上时停止旋转,旋转过程中,
上时停止旋转,旋转过程中,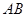 边交直线
边交直线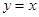 于点
于点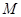 ,
,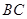 边交
边交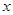 轴于点
轴于点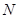
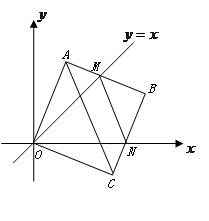
(1)求边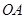 在旋转过程中所扫过的面积;
在旋转过程中所扫过的面积;
(2)旋转过程中,当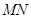 和
和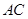 平行时,求正方形
平行时,求正方形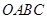 旋转的度数;
旋转的度数;
(3)设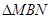 的周长为
的周长为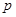 ,在旋转正方形
,在旋转正方形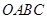 的过程中,
的过程中,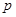 值是否有变化?请证明你的结论.
值是否有变化?请证明你的结论.
如图, 在直角坐标平面上, 点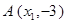 在第三象限, 点
在第三象限, 点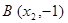 在第四象限, 线段
在第四象限, 线段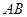 交
交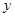 轴于点
轴于点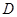 .
. 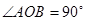 ,
,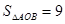 , 设
, 设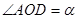 , 求
, 求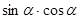 的值.
的值.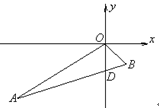
为迎接第四届世界太阳城大会,德州市把主要路段路灯更换为太阳能路灯.已知太阳能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但太阳能路灯的售价不得低于3500元/个.乙店一律按原价的80℅销售.现购买太阳能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)若市政府投资140万元,最多能购买多少个太阳能路灯?
在每年召开的市人代会上, 某市财政局都要报告年度市财政预算和执行情况. 以下是根据
2007~2011年度报告中有关数据制作的市财政教育预算与实际投入统计图表的一部分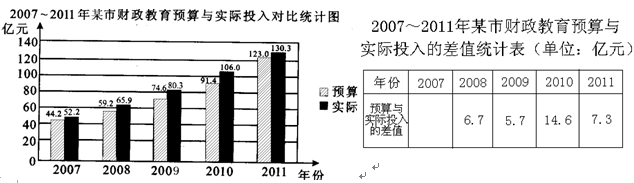
(1)请在表的空格内填入2007年市财政教育实际投入与预算的差值;
(2)求2007~2011年某市财政教育实际投入与预算差值的平均数;
(3)已知2012年某市财政教育预算是141.7亿元, 在此基础上, 如果2012年某市财政教育实际
投入按照(2)中求出的平均数增长, 估计它的金额可能达到多少亿元?