研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
| 球的颜色 |
无记号 |
有记号 |
|
|
| 红色 |
黄色 |
红色 |
黄色 |
|
| 摸到的次数 |
18 |
28 |
2 |
2 |
推测计算:由上述的摸球实验可推算:
(1)盒中红球、黄球各占总球数的百分比分别是多少?
(2)盒中有红球多少个?
小明在做课本“目标与评定”中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?
(1)①请帮小明在图2的画板内画出你的测量方案图(简要说明画法过程);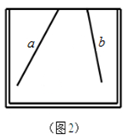
②说出该画法依据的定理.
(2)小明在此基础上进行了更深入的探究,想到两个操作: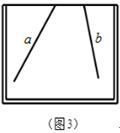
①在图3的画板内,在直线a与直线b上各取一点,使这两点与直线a、b的交点构成等腰三角形(其中交点为顶角的顶点),画出该等腰三角形在画板内的部分.
②在图3的画板内,作出“直线a、b所成的跑到画板外面去的角”的平分线(在画板内的部分),只要求作出图形,并保留作图痕迹.
请你帮小明完成上面两个操作过程.(必须要有方案图,所有的线不能画到画板外,只能画在画板内)
某学校的校门是伸缩门(如图1),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图2);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图3).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.0872,cos5°≈0.9962,sin10°≈0.1736,cos10°≈0.9848).
为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图甲、乙所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:

(1)校团委随机调查了多少学生?请你补全条形统计图;
(2)表示“50元”的扇形的圆心角是多少度?补调查的学生每人一周零花钱数额的中位数是多少元?
(3)四川雅安地震后,全校1000名学生每人自发地捐出一周零花钱的一半,以支援灾区建设.请估算全校学生共捐款多少元?
如图,一次函数y=kx+1(k≠0)与反比例函数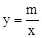 (m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.
(1)求一次函数与反比例函数的解析式;
(2)求△ABC的面积?
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.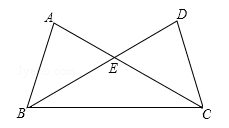
(1)求证:△ABE≌DCE;
(2)当∠AEB=50°,求∠EBC的度数。