小明在做课本“目标与评定”中的一道题：如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？
（1）①请帮小明在图2的画板内画出你的测量方案图（简要说明画法过程）；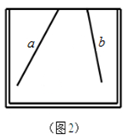
②说出该画法依据的定理．
（2）小明在此基础上进行了更深入的探究，想到两个操作：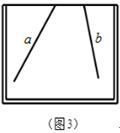
①在图3的画板内，在直线a与直线b上各取一点，使这两点与直线a、b的交点构成等腰三角形（其中交点为顶角的顶点），画出该等腰三角形在画板内的部分．
②在图3的画板内，作出“直线a、b所成的跑到画板外面去的角”的平分线（在画板内的部分），只要求作出图形，并保留作图痕迹．
请你帮小明完成上面两个操作过程．（必须要有方案图，所有的线不能画到画板外，只能画在画板内）
如图，某风景区的湖心岛有一凉亭A，其正东方向有一棵大树B，小明想测量A、B之间的距离，他从湖边的C处测得A在北偏西45°方向上，测得B在北偏东32°方向上，且量得B、C之间的距离为100米，根据上述测量结果，请你帮小明计算A、B之间的距离是多少？（结果精确到1米。参考数据：sin32°＝0．5299，cos32°＝0．8480）
为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况，根据老年人、成年人、青少年各年龄段实际人口的比例3：5：2，随机抽取一定数量的观众进行调查，得到如下统计图．
（1）上面所用的调查方法是（填“全面调查”或“抽样调查”）；
（2）写出折线统计图中A、B所代表的值； A：；B：；
（3）求该地区喜爱娱乐类节目的成年人的人数．
已知△ABC在平面直角坐标系中的位置如图所示．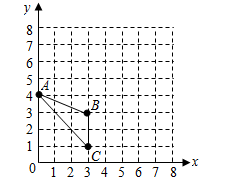
（1）分别写出图中点A和点C的坐标；
（2）画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′；
（3）求点A旋转到点A′所经过的路线长（结果保留π）
如图，二次函数y=-
x2+bx+c的图像经过点A（4,0）B（-4，-4），且与y轴交于点C．
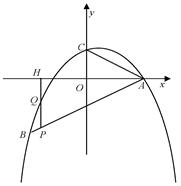
（1）求此二次函数的解析式；
（2）证明：∠BAO=∠CAO（其中O是原点）；
（3）若P是线段AB上的一个动点（不与A、B重合），过P作y轴的平行线，分别交此二次函数图像及x轴于Q、H两点，试问：是否存在这样的点P，使PH=2QH？若存在，请求出点P的坐标；若不存在，请说明理由．
已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF 
（1）如图1，当点D在线段BC上时．求证CF+CD=BC；
（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；
（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；
①请直接写出CF，BC，CD三条线段之间的关系；
②若正方形ADEF的边长为
，对角线AE，DF相交于点O，连接OC．求OC的长度．