如图,∠1=∠2,AC平分∠DAB,求证:DC∥AB.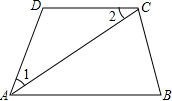
如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)请说明:AB=CD.
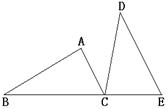
已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
求证: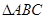 ≌
≌ .
.
解方程:(1)(x+2)2=9;(2)64(x+1)3=27
如图,二次函数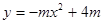 的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
的顶点坐标为(0,2),矩形ABCD的顶点B.C在x轴上,A.D在抛物线上,矩形ABCD在抛物线与x轴所围成的图形内。
(1)求二次函数的解析式;
(2)设点D的坐标为(x,y),试求矩形ABCD的周长P关于自变量x的函数解析式,并求出自变量x的取值范围;
(3)是否存在这样的矩形ABCD,使它的周长为9?试证明你的结论。
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E。求证: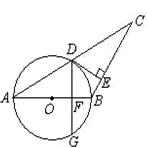
(1)DE是⊙O的切线;
(2)作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8,求弦DG的长。