如图,已知∠1=36°,当∠2等于多少度时,AB∥CD?请说明理由.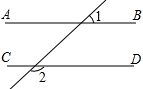
如图,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)
如图,已知点E在平行四边形ABCD的边AD上,AE=3ED,延长CE到点F,使得EF=CE,设 =
= ,
, =
= ,试用
,试用 、
、 分别表示向量
分别表示向量 和
和 .
. 
(本题满分10分, 第(1)小题6分,第(2)小题4分)
已知二次函数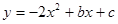 的图像经过点A(0,4)和B(1,-2).
的图像经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
解方程: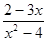 -
- =2.
=2.
(12)如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.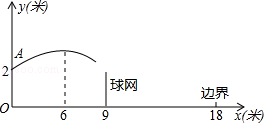
(1)当h=2.6时,求y与x的函数关系式.
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由.
(3)若球一定能越过球网,又不出边界.则h的取值范围是多少?